0 前言

目标跟踪（Object Tracking）是自动驾驶中非常常见的任务，根据跟踪目标数量的不同，目标跟踪可分为：

单目标跟踪（Single Object Tracking，SOT）
多目标跟踪（Multi-Objects Tracking，MOT）

目标跟踪所要做的是根据传感器量测序列确定真实目标的数量以及每个目标的对应状态（位置、速度、航向等），具体实现可大体分为三部分：

状态估计
数据关联
航迹管理

典型的多目标跟踪系统框架如下所示 [1]：

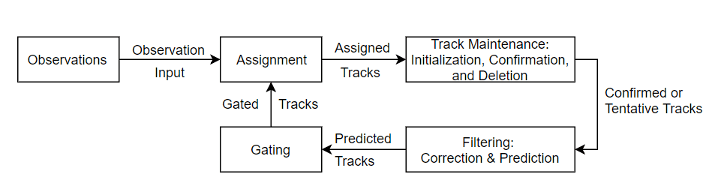
其中，数据关联（Data Association）是目标跟踪中最具挑战的任务之一。对于单目标跟踪而言，数据关联要解决的是传感器量测能否与跟踪目标关联上；对于多目标跟踪而言，数据关联要解决的是哪个传感器量测能与哪个跟踪目标关联上，意即，跟踪目标与传感器量测的一一对应关系。目前，数据关联已发展出多种理论与算法，包括但不限于 [2]：

最近邻（Nearest Neighbor，NN）
概率数据关联（Probability Data Association，PDA）
联合概率数据关联（Joint Probability Data Association，JPDA）
多假设跟踪（Multiple Hypothesis Tracking，MHT）
随机有限集（Random Finite Set，RFS）
匈牙利算法（Hungarian Algorithm）

多目标跟踪数据关联问题可以转化为有权二分图最小权匹配问题，本文将从图论中的一些基本概念出发，对匈牙利算法的发展脉络、算法流程及其 C++ 代码实现进行详细阐述。

1 基本概念

匈牙利算法本质是图算法，所以在对其进行展开前，我们首先需要认识一些图论中重要的基本概念。

1.1 图

图（Graph，G），是由顶点集合（Vertices，V）和边集合（Edges，E）组成的二元组，表征了不同顶点间的拓扑连接关系，记作：

$G=(V,E)$

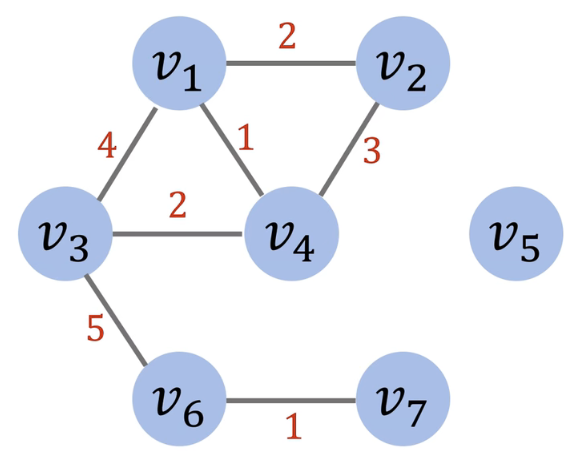
根据图中的边是否具有单向性可将图分为有向图（Directed Graph）和无向图（Undirected Graph），根据图中的边是否具有不同的权重可将图分为有权图（Weighted Graph）和无权图（Unweighted Graph）。本文中将讨论的图都是无向有权图（Undirected Weighted Graph），一个典型的无向有权图如下所示 [3]：

1.2 二分图

1.2.1 二分图的概念

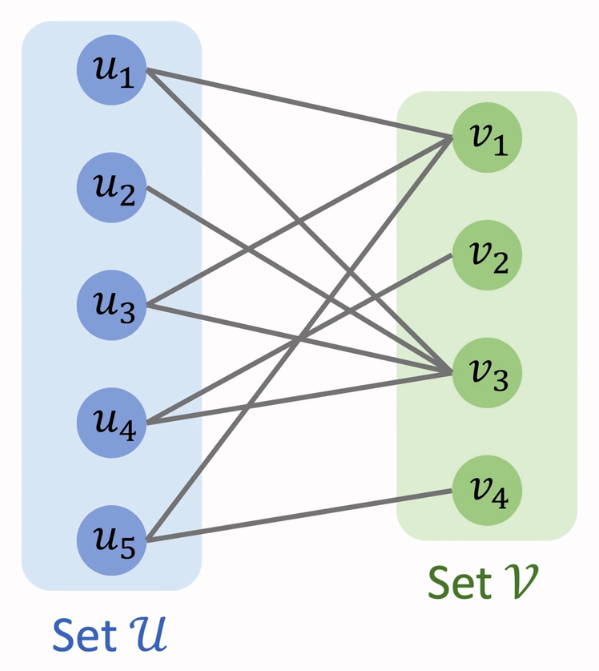
二分图（Bipartite Graph）是一种特殊的图，又称二部图。二分图的顶点集可以被划分为两个互不相交的独立子集 $U$ 和 $V$ [4]：

$G=(U,V,E)$

二分图边集合 $E$ 中的每一条边分别连接了顶点子集 $U$ 和 $V$ 中的一个顶点，但 $U$ 和 $V$ 内部的顶点互不相连。一个典型的二分图如下所示 [5]：

1.2.2 二分图的判定

判定一个图是否是二分图等价于判定该图是否是二色图 [6]，即图中所有顶点是否能被染色成两类颜色（需要保证相连顶点不能同色），我们可以通过广度优先搜索（Breadth First Search，BFS）实现 [7]。下面我们给出具体的 C++ 代码示例，示例中使用邻接表来存储图，时间复杂度 $\mathcal{O}(V+E)$，可以使用菜鸟工具 C++ 在线工具运行并验证程序：

#include <iostream>
#include <vector>
#include <queue>
#include <utility>

/**
 * @brief 用于判断输入的图是否是二分图
 *
 * @param V 图的顶点数量
 * @param adj 图的邻接表表示
 * @return bool 图是否是二分图：true - 是，false - 不是
 */
bool IsBipartite(int V, std::vector<int> adj[])
{
    // 存储所有顶点颜色的 vector 容器，初值 -1 表示未染色，0 表示红色，1 表示蓝色
    std::vector<int> col(V, -1);

    // 用于 BFS 过程的 FIFO 队列，元素类型是顶点索引及其颜色组成的二元组
    std::queue<std::pair<int, int>> q;

    // 遍历所有顶点
    for (int i = 0; i < V; i++)
    {
        // 顶点 i 尚未染色
        if (col[i] == -1)
        {
            // 将顶点 i 染成红色 0，并将其压入 BFS FIFO 队列
            col[i] = 0;
            q.push({ i, 0 });

            // 处理 BFS FIFO 队列中的各顶点
            while (!q.empty())
            {
                auto p = q.front();
                q.pop();

                // 当前顶点
                int v = p.first;
                // 当前顶点的颜色
                int c = p.second;

                // 遍历当前顶点的所有相连顶点
                for (int j : adj[v])
                {
                    // 若相连顶点 j 与当前顶点颜色相同，则输入的图不是二分图
                    if (col[j] == c) return false;

                    // 若相连顶点 j 尚未染色
                    if (col[j] == -1)
                    {
                        // 将相连顶点 j 染成与当前顶点颜色相反的颜色，并将其压入 BFS
                        // FIFO 队列
                        col[j] = 1 - c;
                        q.push({ j, col[j] });
                    }
                }
            }
        }
    }

    return true;
}

int main()
{
    int V, E;
    V = 4 , E = 8;

    // 使用邻接表存储图
    std::vector<int> adj[V];
    adj[0] = {1, 3};
    adj[1] = {0, 2};
    adj[2] = {1, 3};
    adj[3] = {0, 2};


    IsBipartite(V, adj) ? std::cout << "输入的图是二分图" << std::endl
                        : std::cout << "输入的图不是二分图" << std::endl;

    return 0;
}

二分图的判定与本文中要讲解的匈牙利算法并不直接相关，这里只作为二分图概念的扩展内容。

1.3 匹配

给定图 $G=(V,E)$，它的一个匹配（Matching）$M$ 表示包含于边集合 $E$ 的一个子集，即 $M$ 由 $E$ 中的若干条边组成：

$M \subseteq E$

匹配中的任意两条边之间没有公共顶点。以上面的二分图为例，下图中的两条红色边构成了它的一个匹配 [8]：

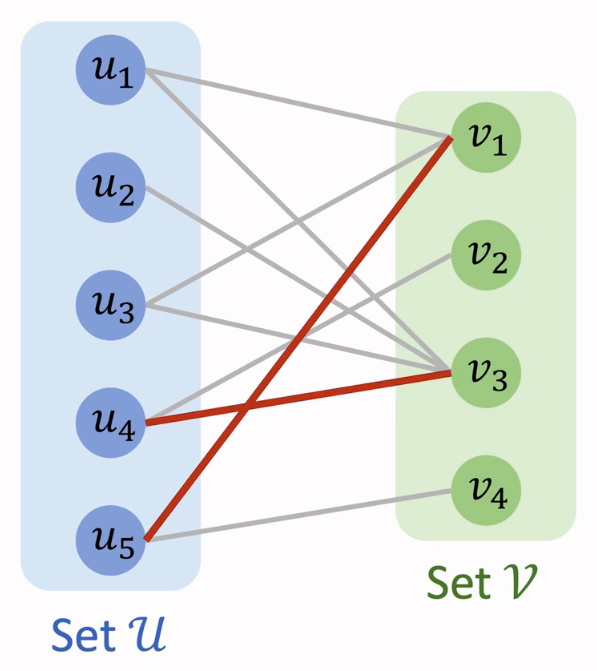
匹配 $M$ 中的边被称为匹配边，上图中的两条红色边都是匹配边；边集合 $E$ 中不属于匹配 $M$ 的边被称为未匹配边，上图中的灰色边都是未匹配边。

匹配边的端点被称为匹配点，上图中顶点 $u_4$、$u_5$、$v_1$、$v_3$ 都是匹配点；顶点集合 $U$ 和 $V$ 中不是匹配边端点的其它顶点被称为未匹配点，上图中顶点 $u_1$、$u_2$、$u_3$、$v_2$、$v_4$ 都是未匹配点。

1.4 最大匹配

最大匹配（Maximum-Cardinality Matching）表示图的所有匹配中边数最多的那些匹配。最大匹配不唯一，仍以上面的二分图为例，它的最大匹配的边数为 4，下面的两个匹配都是它的最大匹配 [8]：

1.5 最大权匹配和最小权匹配

最大权匹配（Maximum-Weight Matching）表示的是有权图的所有匹配中边的权重之和最大的那些匹配，最小权匹配（Minimum-Weight Matching）表示的是有权图的所有匹配中边的权重之和最小的那些匹配。

仍以上面的二分图为例，我们为它所有的边赋上权重，将其转化为有权二分图 [9]：

对于上面的有权二分图，我们将任意边上的权重记作 $w$，任意匹配记作 $M$，匹配 $M$ 包含的所有匹配边的权重和记作函数 $f(M)$，则有权二分图的最大权匹配（Maximum-Weight Bipartite Matching）问题和有权二分图的最小权匹配（Minimum-Weight Bipartite Matching）问题可以用如下数学语言进行描述：

$\begin{cases} f(M)=\displaystyle\sum_{(u,v) \in M}{w_{u,v}} \\ \max / \min{f(M)} \end{cases}$

多目标跟踪数据关联问题可以转化为有权二分图最小权匹配问题，跟踪过程中的航迹序列和量测序列可以分别看作是上面这个有权二分图中的顶点集合 $U$ 和 $V$，边的权重可以看作是航迹和量测间通过某种方式计算得到的匹配距离（例如欧式距离），这个匹配距离我们称之为代价（Cost），所有的匹配距离构成了代价矩阵（Cost Matrix），我们需要做的是，找到航迹和量测间的匹配关系使得总的匹配距离最小（代价最低）。

1.6 交替路

给定图 $G=(V,E)$ 和它的一个匹配 $M$，交替路（Alternating Path）描述的是图中的这样一条路径：从图中的某个未匹配点出发，交替经过未匹配边和匹配边形成的路径。下面的二分图中，路径 $u_3$ $\color{gray}{\rightarrow}$ $v_1$ $\color{red}{\rightarrow}$ $u_1$ $\color{gray}{\rightarrow}$ $v_3$ $\color{red}{\rightarrow}$ $u_2$ 就是一条交替路：

1.7 增广路

1.7.1 增广路的概念

增广路（Augmenting Path）是一条特殊的交替路，增广路从图中的某个未匹配点起始，交替经过未匹配边和匹配边，并终止于不同于起始点的另一个未匹配点。下面的二分图中，路径 $u_1$ $\color{gray}{\rightarrow}$ $v_1$ $\color{red}{\rightarrow}$ $u_5$ $\color{gray}{\rightarrow}$ $v_4$ 就是一条增广路：

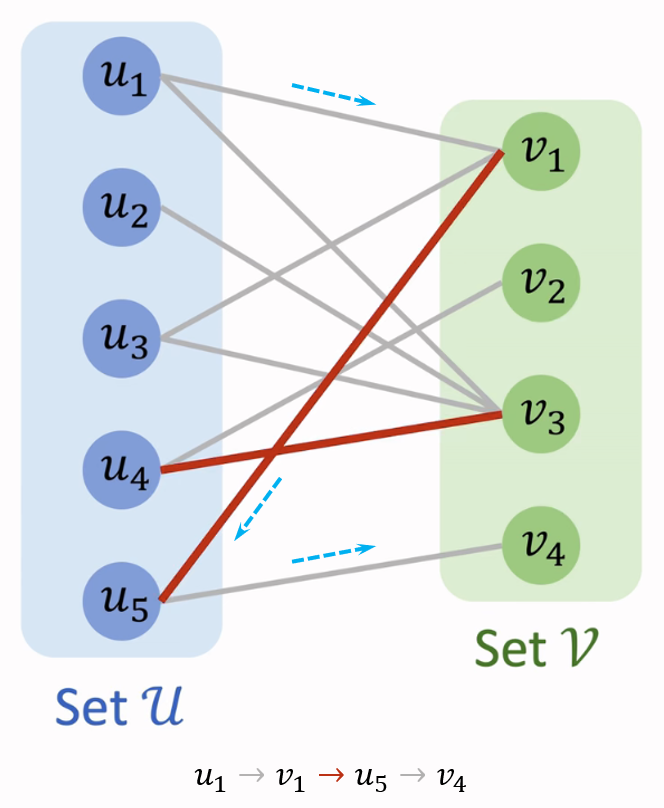
1.7.2 增广路的性质

给定图 $G=(V,E)$ 和它的一个匹配 $M$ 以及增广路 $P$，并将 $P$ 上所有的边记作集合 $E_P$，则有如下三个非常重要的性质：

Berge 定理：对于给定的图 $G$ 和它的一个匹配 $M$，$M$ 是 $G$ 的最大匹配的充要条件是 $G$ 中不存在匹配 $M$ 的增广路 [10]；
$E_P$ 中边的数量一定为奇数，且增广路 $P$ 的第奇数条边不属于匹配 $M$，第偶数条边属于匹配 $M$，这意味着，$E_P$ 中的未匹配边数量一定比匹配边数量多 1；
通过性质 2 不难发现，通过将 $E_P$ 中的未匹配边取反变成匹配边，匹配边取反变成未匹配边，就可以多出 1 条匹配边，取反得到的新匹配边和 $M$ 中不属于 $E_P$ 的剩余边可以构成一个更大的匹配 $M’$。在集合论中，$M’$ 被称作 $M$ 和 $E_P$ 的对称差（Symmetric Difference）[11]，记作 $M\ominus E_P$：

$M\ominus E_P=(M\cup E_P) - (M\cap E_P)$

结合性质 1 和性质 3 我们不难发现，对于一个给定的二分图 $G=(U,V,E)$ 和初始为空的匹配 $M$，我们只要反复搜索增广路就能逐渐扩展匹配的大小，最终当我们找不到增广路时就得到了一个最大匹配，下图中的示例很直观地展示了这个过程：

最后得到的 $M=\{e_{1,3},e_{3,1},e_{4,2},e_{5,4}\}$ 就是输入二分图 $G$ 的一个最大匹配。很多资料中使用“婚配问题”为例来讲解上述过程 [12]，这里我们不再赘述，一句话总结：有机会上，没机会创造机会也要上。

2 匈牙利算法的发展脉络

匈牙利算法是全局最近邻（Global Nearest Neighbor，GNN）数据关联思想的一种具体实现，其最早用于求解经济学领域中的任务分配问题，后来发展成为图论领域中求解有权二分图最小权匹配问题的一般性算法 [13] [14] [15]：

1955 年，Harold Kuhn 在匈牙利数学家 Dénes Kőnig 和 Jenő Egerváry 的研究基础（系数矩阵中独立 0 元素的最多个数等于能覆盖所有 0 元素的最少直线数）上提出了匈牙利方法（Hungarian Method）以求解任务分配问题 [16]。
1956 年，Harold Kuhn 通过图论重新建模了使用匈牙利方法求解任务分配问题的过程，并将任务分配问题转化为有权二分图最小权匹配问题，同时比较了匈牙利方法的几个变种 [17]。
1956 年，Merrill M. Flood 给出了匈牙利方法的算法实现步骤（划线法：划最少的线覆盖所有的 0），这是原始的匈牙利算法，网络上很多讲解匈牙利算法的资料中都使用了这里的步骤 [18]。
1957 年，James Munkres 回顾并改进了匈牙利方法，针对划线法首次引入“标星 0（starred zeros）”和“标撇 0（primed zeros）”的概念，自此该算法常被称为 Kuhn–Munkres 算法、KM 算法或 Munkres 分配算法 [19]。Kuhn–Munkres 算法只适用于分配矩阵（关联矩阵）为方阵的情形（即 $|U|=|V|$），最坏时间复杂度 $\mathcal{O}(n^4)$。
1957 年，法国数学家 Claude Berge 证明，对于给定的图 $G$ 和它的一个匹配 $M$，$M$ 是最大匹配的充要条件是图中不存在匹配 $M$ 的增广路——Berge 定理 [10]，该定理奠定了后来各种通过搜索增广路求解图最大匹配问题的基础。
1965 年，组合优化大师 Jack Edmonds [20] 提出“带花树开花”算法（Blossom Algorithm）[21]，用于求解无权一般图最大匹配问题 [22] 和有权一般图最大权匹配问题 [23]，算法基于 Berge 定理通过反复搜索增广路来逐渐扩展部分匹配，直至找不到增广路。
1971 年，François Bourgeois 等人将 Kuhn–Munkres 算法扩展到分配矩阵为非方阵的情形 [24]。
1973 年，John Hopcroft 和 Richard Karp 提出 Hopcroft–Karp 算法[25]，用于求解无权二分图最大匹配问题，类似 Blossom 算法，Hopcroft–Karp 算法同样是通过反复搜索增广路的方式来逐渐扩展部分匹配，不同的是该算法每次迭代可以得到多条增广路，因而算法效率更高 [26]。
1978 年，JIN KUE WONG 将 Kuhn–Munkres 算法的最坏时间复杂度优化到 $\mathcal{O}(n^3)$ [27]。

通过网络搜索匈牙利算法相关资料时，我们经常会看到一些有误导性的说法，例如“匈牙利算法用于求解无权二分图的最大匹配问题，1965 年由匈牙利数学家 Edmonds 提出，故得名匈牙利算法；KM 算法用于求解有权二分图的最小权匹配问题” [28]，类似说法很不严谨且容易让人产生混淆。根据匈牙利算法的发展历程，我们给出下面的三个事实对这些说法予以反驳：

现在常说的以及文献中常提到的匈牙利算法和 Kuhn-Munkres 算法指的是同一个东西，求解的都是有权二分图最小权匹配问题；
匈牙利算法起源于 1955 年 Kuhn 提出的匈牙利方法（Hungarian Method），1956 年 Merrill M. Flood 给出了匈牙利方法的算法实现步骤，1957 年 Munkres 针对该方法做了改进，后来大家习惯叫匈牙利算法或 Kuhn-Munkres 算法；
Edmonds 1965 年提出的是用于求解一般图最大匹配和最大权匹配的“带花树开花”算法（Blossoms Algorithm），算法基于 Berge 定理通过反复搜索增广路的方法来逐渐扩展部分匹配，后来这个方法被引入了我们现在经常看到的各种版本的匈牙利算法代码实现。

自始至终，反复搜索增广路扩展部分匹配都是一种基于 Berge 定理的用于求解图最大匹配问题的方法，而非匈牙利算法本身。

除匈牙利算法外，Jonker-Volgenant 算法 [29]、Auction 算法 [30] 等也可用于求解分配问题，这三个算法也是 Matlab GNN 跟踪器 trackerGNN [31] 可选的分配算法，这里我们不做展开。

3 原始匈牙利算法

3.1 算法流程

上文中我们已经提到，匈牙利算法的原始流程由 Merrill M. Flood 于 1956 年给出。假设代价矩阵为 $n\times n$ 的方阵（航迹、量测数量相同），则原始流程步骤如下图所示：

3.2 操作示例

假设我们有下面的 $4\times 4$ 航迹量测代价矩阵，矩阵中的元素表示航迹量测间的匹配距离（实际项目中匹配距离不会这么夸张，这里只为演示）：

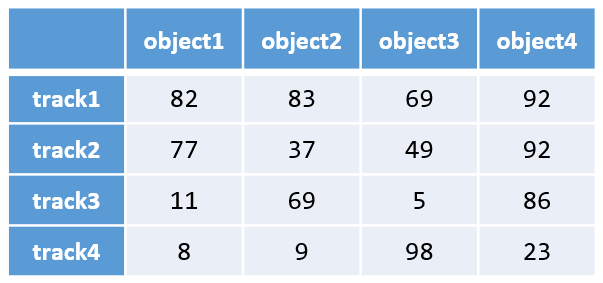
我们将上述的匈牙利算法原始流程步骤应用到该代价矩阵上，则求解其最小权匹配的流程如下图所示：

最后需要划 4 条线才能覆盖住矩阵中所有的 0 元素，迭代终止，根据矩阵中 0 元素的位置我们很容易得到航迹量测最终的匹配关系：track1→object3，track2→object2，track3→object1，track4→object4。这个匹配满足航迹量测构成的二分图上的匹配边总权重最小，即总的匹配距离最小，代价最低。

二分图最大权匹配问题可以与最小权匹配问题相互转化。假设上述代价矩阵中的各元素表示航迹量测间的相似度得分，我们想要找到航迹量测的某个匹配关系使得总的相似度得分最高，这显然是一个二分图最大权匹配问题。首先，我们找到原代价矩阵中的最大代价，并将原代价矩阵中每个元素替换为最大代价与对应元素的差值以得到新的代价矩阵，这样代价矩阵中元素间的相对大小关系就发生了反转：

然后，在新的代价矩阵上执行前文中的二分图最小权匹配求解流程即可，得到的匹配结果即为原代价矩阵的最大权匹配。

4 改进的 KM 算法

4.1 算法流程

上述匈牙利算法原始流程虽然直观易懂，但在代码实现上并不容易，其中的一个关键难点是：如何用尽量少的线覆盖代价矩阵中所有的 0？

前文中已经提到，1957 年 James Munkres 引入了“标星 0（starred zeros）”和“标撇 0（primed zeros）”的概念以改进匈牙利算法原始流程中的划线法，在算法执行过程中会选择性地对代价矩阵中产生的 0 元素标记星号（*）或标记撇号（’）来辅助搜索增广路，标星 0 表示增广路中的匹配边，标撇 0 表示增广路中的未匹配边。后来我们习惯将 Munkres 提出的方法称为 Kuhn–Munkres 算法、KM 算法或 Munkres 分配算法。

KM 算法本身只适用于代价矩阵为方阵的情形，本文将介绍一种 KM 算法的改进版本 [32]，这里我们姑且称之为 MKM（Modified Kuhn–Munkres）算法。MKM 算法已被大量运用于工业实践，例如 Matlab 中的 Hungarian Algorithm for Linear Assignment Problems [33] 、Python 中的 munkres 包 [34] 以及百度 Apollo 自动驾驶框架中的 Hungarian Optimizer [35] [36]。MKM 通过“膨胀补 0”的方式来处理代价矩阵为非方阵的情形，例如，如果代价矩阵维度为 $4\times 3$，则 MKM 会为代价矩阵额外补充一个 0 元素列使之成为方阵。Apollo Hungarian Optimizer 中应用的 MKM 算法流程如下图所示：

可见，MKM 中也使用了反复搜索增广路的方式来逐步扩展部分匹配。此外，MKM 的步骤 6 与匈牙利算法原始流程中的步骤 4 是等价的。

4.2 操作示例

为演示 MKM 的操作流程，假设我们的航迹量测代价矩阵是个 $4\times 3$ 的非方阵（4 个航迹 3 个量测，意味着传感器出现了漏检）：

我们将上述的 MKM 算法流程步骤应用到该代价矩阵上，则求解其最小权匹配的流程如下图所示：

最终根据矩阵中标星 0 的位置我们就可以得到航迹量测的匹配关系：track2→object2，track3→object3，track4→object1，至于 track1，没有找到与它匹配的量测。这个匹配满足航迹量测构成的二分图上的匹配边总权重最小，即总的匹配距离最小，代价最低。

对于代价矩阵为非方阵的二分图最大权匹配问题，我们同样可以像前文所述的那样首先对其进行转化，然后再实施 MKM 算法流程求解最小权匹配问题即可。

4.3 代码实现

这里我们抽取了 Apollo Hungarian Optimizer 的关键代码并整理成了一个 C++ demo 示例，主要的算法代码是一个名为 HungarianOptimizer 的模板类，该模板类具备如下主要特性：

适配代价矩阵为非方阵的情形
可求解最小权匹配问题
可求解最大权匹配问题
可输出部分匹配

可以点击这里查看 GitHub 项目主页，编译工程后运行可执行程序可以得到下面的终端打印结果：

The assignments are:

    (1, 1)
    (2, 2)
    (3, 0)

这里的结果是代价矩阵行列索引（从 0 开始）间的匹配关系，将其映射成 track id 和 object id 后会发现与我们上文中的手动演算结果一致。

需要说明的是，Apollo 在优化给定的航迹量测代价矩阵前，会首先将其切割为多个连通子图，然后对每个连通子图分别实施 MKM 流程，以达到提升效率的目的。这里我们只关心 MKM 的核心算法流程，所以省略了这一步骤，直接对给定的代价矩阵进行最小权匹配求解。

程序入口：main

示例工程的主入口如下所示，

int main() {
  std::vector<std::vector<float>> association_mat = {{82.0f, 83.0f, 69.0f},
                                                     {77.0f, 37.0f, 49.0f},
                                                     {11.0f, 69.0f, 5.0f},
                                                     {8.0f, 9.0f, 98.0f}};
  HungarianOptimizer<float> optimizer;
  std::vector<std::pair<size_t, size_t>> assignments;

  UpdateCosts(association_mat, optimizer.costs());

  // entry of hungarian optimizer minimum-weighted matching
  optimizer.Minimize(&assignments);

  PrintAssignments(assignments);

  return 0;
}

main 函数主要做了四件事：

设定代价矩阵
更新 HungarianOptimizer 内部代价
最小权匹配问题求解
打印航迹量测关联结果

MKM 最小权匹配入口：Minimize

Minimize 函数是 HungarianOptimizer 的最小权匹配问题求解入口：

/* Find an assignment which minimizes the overall costs.
 * Return an array of pairs of integers. Each pair (i, j) corresponds to
 * assigning agent i to task j. */
template <typename T>
void HungarianOptimizer<T>::Minimize(
    std::vector<std::pair<size_t, size_t>>* assignments) {
  OptimizationInit();
  DoMunkres();
  FindAssignments(assignments);
  OptimizationClear();
}

Minimize 函数主要做了四件事：

算法初始化 OptimizationInit：对应我们上文中提到的 MKM 初始化步
运行算法主流程 DoMunkres：对应我们上文中提到的 MKM 步骤 1 到步骤 6
生成匹配结果 FindAssignments
清除初始化标志 OptimizationClear

需要说明的是，HungarianOptimizer 同样可以用于求解最大权匹配问题，对原代价矩阵直接调用其 Maximize 函数即可。

下面我们对 OptimizationInit 和 DoMunkres 的代码实现进行简要讲解并给出必要的中文注释。

4.3.1 算法初始化

OptimizationInit 函数对应了我们上文中提到的 MKM 初始化步，其主要完成了代价矩阵“膨胀补 0”、代价矩阵标记初始化、增广路初始化等工作。

template <typename T>
void HungarianOptimizer<T>::OptimizationInit() {
  // 已完成初始化，返回
  if (optimization_initialized_) {
    return;
  }
  width_ = costs_.width();
  if (width_ > 0) {
    height_ = costs_.height();
  } else {
    height_ = 0;
  }

  matrix_size_ = std::max(height_, width_);
  max_cost_ = 0;

  /* generate the expanded cost matrix by adding extra 0s in order to make a
   * square matrix. Meanwhile, find the max cost in the matrix. It may be used
   * later, if we want to maximizing rather than minimizing the overall costs.*/
  // 代价矩阵膨胀补 0，确保代价矩阵为方阵
  costs_.Resize(matrix_size_, matrix_size_);
  for (size_t row = 0; row < matrix_size_; ++row) {
    for (size_t col = 0; col < matrix_size_; ++col) {
      if ((row >= height_) || (col >= width_)) {
        costs_(row, col) = 0;
      } else {
        max_cost_ = std::max(max_cost_, costs_(row, col));
      }
    }
  }

  /* initially, none of the cells of the matrix are marked. */
  // 代价矩阵标记初始化
  marks_.Resize(matrix_size_, matrix_size_);
  for (size_t row = 0; row < matrix_size_; ++row) {
    for (size_t col = 0; col < matrix_size_; ++col) {
      marks_(row, col) = Mark::NONE;
    }
  }

  stars_in_col_.assign(matrix_size_, 0);

  rows_covered_.assign(matrix_size_, false);
  cols_covered_.assign(matrix_size_, false);

  // 增广路初始化
  assignments_.resize(matrix_size_ * 2);
  // 初始化化标志置 true
  optimization_initialized_ = true;
}

4.3.2 算法主流程

主流程入口：DoMunkres

DoMunkres 函数对应了我们上文中提到的 MKM 步骤 1 到步骤 6，步骤循环迭代，求解成功或达到指定迭代次数阈值结束循环。同时，若达到指定迭代次数阈值，则取消最终的代价矩阵中存在不止一个标星 0 的行里的所有星号标记，以实现部分匹配输出。

/* Run the Munkres algorithm */
template <typename T>
void HungarianOptimizer<T>::DoMunkres() {
  int max_num_iter = 1000;
  int num_iter = 0;
  // fn_state_ 代表算法当前状态，即执行到了哪一步
  fn_state_ = std::bind(&HungarianOptimizer::ReduceRows, this);
  // 从步骤 1 开始循环迭代，直至求解成功或达到指定迭代次数阈值
  while (fn_state_ != nullptr && num_iter < max_num_iter) {
    fn_state_();
    ++num_iter;
  }
  /* 若达到指定迭代次数阈值，则取消最终的代价矩阵中存在不止一个标星 0 的行里的所有星号
   * 标记，实现部分匹配输出 */
  if (num_iter >= max_num_iter) {
    CheckStar();
  }
}

步骤 1：ReduceRows

代价矩阵的每一行元素减去该行元素中的最小值，然后执行步骤 2。

/* Step 1:
 * For each row of the matrix, find the smallest element and substract it
 * from every element in its row. Then, go to Step 2. */
template <typename T>
void HungarianOptimizer<T>::ReduceRows() {
  for (size_t row = 0; row < matrix_size_; ++row) {
    T min_cost = costs_(row, 0);
    for (size_t col = 1; col < matrix_size_; ++col) {
      min_cost = std::min(min_cost, costs_(row, col));
    }
    for (size_t col = 0; col < matrix_size_; ++col) {
      costs_(row, col) -= min_cost;
    }
  }
  // 执行步骤 2
  fn_state_ = std::bind(&HungarianOptimizer::StarZeroes, this);
}

步骤 2：StarZeroes

对代价矩阵中所在行和列中都没有标星 0 的 0 元素标记星号 *，然后执行步骤 3。

/* Step 2:
 * Find a zero Z in the matrix. If there is no starred zero in its row
 * or column, star Z. Repeat for every element in the matrix. Then, go to
 * Step3. */
template <typename T>
void HungarianOptimizer<T>::StarZeroes() {
  /* since no rows or columns are covered on entry to this step, we use the
   * covers as a quick way of making which rows & columns have stars in them */
  for (size_t row = 0; row < matrix_size_; ++row) {
    if (RowCovered(row)) {
      continue;
    }
    for (size_t col = 0; col < matrix_size_; ++col) {
      if (ColCovered(col)) {
        continue;
      }
      if (costs_(row, col) == 0) {
        Star(row, col);
        CoverRow(row);
        CoverCol(col);
        break;
      }
    }
  }
  ClearCovers();
  // 执行步骤 3
  fn_state_ = std::bind(&HungarianOptimizer::CoverStarredZeroes, this);
}

步骤 3：CoverStarredZeroes

覆盖代价矩阵中所有含有标星 0 的列，若所有的列都已被覆盖则结束迭代，否则执行步骤 4。

/* Step 3:
 * Cover each column containing a starred zero. If all columns are covered,
 * the starred zeros describe a complete set of unique assignments. In this
 * case, terminate the algorithm. Otherwise, go to Step 4. */
template <typename T>
void HungarianOptimizer<T>::CoverStarredZeroes() {
  size_t num_covered = 0;
  // 统计被覆盖的列的数量
  for (size_t col = 0; col < matrix_size_; ++col) {
    if (ColContainsStar(col)) {
      CoverCol(col);
      num_covered++;
    }
  }
  // 若所有的列都已被覆盖则结束迭代
  if (num_covered >= matrix_size_) {
    fn_state_ = nullptr;
    return;
  }
  // 执行步骤 4
  fn_state_ = std::bind(&HungarianOptimizer::PrimeZeroes, this);
}

步骤 4：PrimeZeroes

查找当前代价矩阵中是否存在未被覆盖的 0 元素：

存在：对未被覆盖的 0 元素标记撇号 ’，并判断标撇 0 所在的行是否含有标星 0
- 含有：覆盖标撇 0 所在的行，取消覆盖标撇 0 所在行里的标星 0 所在的列，继续查找当前代价矩阵中是否存在未被覆盖的 0 元素
- 不含有：将该标撇 0 置为增广路的首条边，执行步骤 5
不存在：执行步骤 6

/* Step 4:
 * Find a noncovered zero and prime it. If there is no starred zero in the
 * row containing this primed zero, go to Step 5. Otherwise, cover this row
 * and uncover the column containing the starred zero. Continue in this manner
 * until there are no uncovered zeros left, then go to Step 6. */
template <typename T>
void HungarianOptimizer<T>::PrimeZeroes() {
  // this loop is guaranteed to terminate in at most matrix_size_ iterations,
  // as FindZero() returns a location only if there is at least one uncovered
  // zero in the matrix.  Each iteration, either one row is covered or the
  // loop terminates.  Since there are matrix_size_ rows, after that many
  // iterations there are no uncovered cells and hence no uncovered zeroes,
  // so the loop terminates.
  for (;;) {
    size_t zero_row = 0;
    size_t zero_col = 0;
    // 若当前的代价矩阵不存在未被覆盖的 0
    if (!FindZero(&zero_row, &zero_col)) {
      // No uncovered zeroes.
      // 执行步骤 6
      fn_state_ = std::bind(&HungarianOptimizer::AugmentPath, this);
      return;
    }
    // 对未被覆盖的 0 标记撇号
    Prime(zero_row, zero_col);
    int star_col = FindStarInRow(zero_row);
    // 若标撇 0 所在的行含有标星 0
    if (star_col != kHungarianOptimizerColNotFound) {
      // 覆盖标撇 0 所在的行
      CoverRow(zero_row);
      // 取消覆盖标撇 0 所在行里的标星 0 所在的列
      UncoverCol(star_col);
    } else { // 若标撇 0 所在的行不含有标星 0
      std::pair<size_t, size_t> first_assignment =
          std::make_pair(zero_row, zero_col);
      // 将该标撇 0 置为增广路的首条边
      assignments_[0] = first_assignment;
      // 执行步骤 5
      fn_state_ = std::bind(&HungarianOptimizer::MakeAugmentingPath, this);
      return;
    }
  }
}

步骤 5：MakeAugmentingPath

首先，构建增广路，从增广路首条边开始，若标撇 0 所在列存在标星 0 则将该标星 0 置为增广路当前边的下一条边，若标星 0 所在行存在标撇 0 则将该标撇 0 置为增广路当前边的下一条边，直至找不到新的标星 0；然后，执行增广操作，取消增广路中标星 0 的标记，并将增广路中的标撇 0 重新标记为标星 0；最后，取消代价矩阵中的所有行列覆盖，清除代价矩阵中所有标撇 0 的标记，返回步骤 3。

/* Step 5:
 * Construct a series of alternating primed and starred zeros as follows.
 * Let Z0 represent the uncovered primed zero found in Step 4.  Let Z1 denote
 * the starred zero in the column of Z0 (if any). Let Z2 denote the primed
 * zero in the row of Z1 (there will always be one).  Continue until the
 * series terminates at a primed zero that has no starred zero in its column.
 * unstar each starred zero of the series, star each primed zero of the
 * series, erase all primes and uncover every line in the matrix. Return to
 * Step 3. */
template <typename T>
void HungarianOptimizer<T>::MakeAugmentingPath() {
  bool done = false;
  size_t count = 0;

  /* note: this loop is guaranteed to terminate within matrix_size_ iterations
   * because:
   * 1) on entry to this step, there is at least 1 column with no starred zero
   *    (otherwise we would have terminated the algorithm already.)
   * 2) each row containing a star also contains exactly one primed zero.
   * 4) each column contains at most one starred zero.
   *
   * Since the path_ we construct visits primed and starred zeroes alternately,
   * and terminates if we reach a primed zero in a column with no star, our
   * path_ must either contain matrix_size_ or fewer stars (in which case the
   * loop iterates fewer than matrix_size_ times), or it contains more.  In
   * that case, because (1) implies that there are fewer than matrix_size_
   * stars, we must have visited at least one star more than once. Consider
   * the first such star that we visit more than once; it must have been reached
   * immediately after visiting a prime in the same row.  By (2), this prime
   * is unique and so must have also been visited more than once.
   * Therefore, that prime must be in the same column as a star that has been
   * visited more than once, contradicting the assumption that we chose the
   * first multiply visited star, or it must be in the same column as more
   * than one star, contradicting (3). Therefore, we never visit any star
   * more than once and the loop terminates within matrix_size_ iterations. */
  // 构造增广路
  while (!done) {
    /* first construct the alternating path... */
    // 标撇 0 所在的列查找标星 0
    int row = FindStarInCol(assignments_[count].second);
    // 标撇 0 所在的列含有标星 0
    if (row != kHungarianOptimizerRowNotFound) {
      // 增广路游标加 1
      count++;
      // 找到的标星 0 置为标撇 0 的下一条边
      assignments_[count].first = row;
      assignments_[count].second = assignments_[count - 1].second;
    } else { // 标撇 0 所在的列不含有标星 0，增广路构造终止
      done = true;
    }
    // 若增广路构造尚未终止
    if (!done) {
      // 标星 0 所在的行查找标撇 0
      int col = FindPrimeInRow(assignments_[count].first);
      // 增广路游标加 1
      count++;
      // 找到的标撇 0 置为标星 0 的下一条边
      assignments_[count].first = assignments_[count - 1].first;
      assignments_[count].second = col;
    }
  }

  /* then, modify it. */
  // 增广操作：遍历增广路中的每一个 0 元素（代表一条匹配边或未匹配边）
  for (size_t i = 0; i <= count; ++i) {
    size_t row = assignments_[i].first;
    size_t col = assignments_[i].second;
    // 若当前 0 标记了星号（增广路中的匹配边）
    if (IsStarred(row, col)) {
      // 取消当前标星 0 的星号标记（变成全局未匹配边）
      Unstar(row, col);
    } else { // 若当前 0 标记了撇号（增广路中的未匹配边）
      // 将当前标撇 0 重新标记为标星 0（变成匹配边）
      Star(row, col);
    }
  }
  // 取消代价矩阵中的所有行列覆盖
  ClearCovers();
  // 清除代价矩阵中所有标撇 0 的标记
  ClearPrimes();
  // 返回步骤 3
  fn_state_ = std::bind(&HungarianOptimizer::CoverStarredZeroes, this);
}

步骤 6：AugmentPath

查找未被覆盖元素中的最小值 minval，被覆盖行中的每一个元素加上 minval，未被覆盖列中的每一个元素减去 minval。

/* Step 6:
 * Add the smallest uncovered value in the matrix to every element of each
 * covered row, and subtract it from every element of each uncovered column.
 * Return to Step 4 without altering any stars, primes, or covered lines. */
template <typename T>
void HungarianOptimizer<T>::AugmentPath() {
  // 查找未被覆盖元素中的最小值 minval
  T minval = FindSmallestUncovered();
  // 被覆盖行中的每一个元素加上 minval
  for (size_t row = 0; row < matrix_size_; ++row) {
    if (RowCovered(row)) {
      for (size_t c = 0; c < matrix_size_; ++c) {
        costs_(row, c) += minval;
      }
    }
  }
  // 未被覆盖列中的每一个元素减去 minval
  for (size_t col = 0; col < matrix_size_; ++col) {
    if (!ColCovered(col)) {
      for (size_t r = 0; r < matrix_size_; ++r) {
        costs_(r, col) -= minval;
      }
    }
  }
  // 返回步骤 4
  fn_state_ = std::bind(&HungarianOptimizer::PrimeZeroes, this);
}

4.3.3 生成匹配结果

完成最小权匹配问题求解后，需要遍历最终的代价矩阵中的所有元素，根据矩阵中标星 0 的行索引和列索引即可生成航迹量测匹配关系。

/* Convert the final costs matrix into a set of assignments of agents to tasks.
 * Return an array of pairs of integers, the same as the return values of
 * Minimize() and Maximize() */
template <typename T>
void HungarianOptimizer<T>::FindAssignments(
    std::vector<std::pair<size_t, size_t>>* assignments) {
  assignments->clear();
  for (size_t row = 0; row < height_; ++row) {
    for (size_t col = 0; col < width_; ++col) {
      if (IsStarred(row, col)) {
        assignments->push_back(std::make_pair(row, col));
        break;
      }
    }
  }
}

4.3.4 清除初始化标志

实际工程开发中，当前帧信息处理完成后，需要将初始化标志置 false，以使得处理下一帧信息时重新执行初始化操作，因为不同帧间的代价矩阵一般来说是不同的。

template <typename T>
void HungarianOptimizer<T>::OptimizationClear() {
  optimization_initialized_ = false;
}

至此，Apollo Hungarian Optimizer 核心代码分析结束。

5 后记

首先，本文给出了图论中的一些基本概念并由此引出了二分图最大权匹配问题与最小权匹配问题；然后，通过大量原始参考文献厘清了匈牙利算法的发展脉络，并驳斥了一些具有误导性的说法；其次，给出了匈牙利算法的原始流程与操作示例；最后，给出了改进的 KM 算法流程以及一个非方阵代价矩阵的操作示例，并基于 Apollo Hungarian Optimizer 给出了具体的代码实现。

参考

Introduction to Multiple Target Tracking
Introduction to Assignment Methods in Tracking Systems
图的基本概念和数据结构 Graph Basics and Data Structures
Bipartite Graph
二部图及其判定算法 Bipartite Graphs
Graph coloring
Check whether a given graph is Bipartite or not
无权二部图中的最大匹配 Maximum-Cardinality Bipartite Matching (MCBM)
有权二部图中的最大匹配 Maximum-Weight Bipartite Matching
Berge’s theorem
Symmetric difference
趣写算法系列之—匈牙利算法
Hungarian algorithm
Design and Analysis of Modern Tracking Systems
Efficient Algorithms for Finding Maximum Matching in Graphs
The Hungarian method for the assignment problem
VARIANTS OF THE HUNGARIAN METHOD FOR ASSIGNMENT PROBLEMS
THE TRAVELING-SALESMAN PROBLEM
Algorithms for the Assignment and Transportation Problems
Jack Edmonds
Blossom Algorithm
PATHS, TREES, AND FLOWERS
Maximum Matching and a Polyhedron With 0,1-Vertices
An Extension of the Munkres Algorithm for the Assignment Problem to Rectangular Matrices
Hopcroft–Karp algorithm
An n5/2 algorithm for maximum matchings in bipartite graphs
A NEW IMPLEMENTATION OF AN ALGORITHM FOR THE OPTIMAL ASSIGNMENT PROBLEM: AN IMPROVED VERSION OF MUNKRES’ ALGORITHM
带你入门多目标跟踪（三）匈牙利算法 & KM 算法
A Shortest Augmenting Path Algorithm for Dense and Sparse Linear Assignment Problems
The Auction Algorithm for Assignment and Other Network Flow Problem
Matlab GNN 跟踪器 trackerGNN
Munkres’ Assignment Algorithm-Modified for Rectangular Matrices
Hungarian Algorithm for Linear Assignment Problems
munkres — Munkres implementation for Python
Apollo HM 对象跟踪
Apollo Hungarian Optimizer
Inside the Hungarian Algorithm: A Self-Driving Car Example
Apollo perception 源码阅读 | fusion 之匈牙利算法
二分图最大匹配问题与匈牙利算法的核心思想
COS 423 Lecture 19 Graph Matching - cs.Princeton
二部图最大匹配——新数据结构 Augmenting graph 与 Hopcroft-Karp 算法的复杂度证明
匈牙利算法简介
The Assignment Problem (Using Hungarian Algorithm)
指派问题：匈牙利算法
匈牙利算法 Hungarian Algorithm
目标跟踪初探（DeepSORT）
The Hungarian algorithm: An example

输出倒逼思考

多目标跟踪数据关联之匈牙利算法

目录