（十二）无人驾驶中的坐标转换

本文章学习总结自知乎大 V陈光的《无人驾驶干货铺》专栏，查阅原文请移步这里

1 正文

车辆坐标系的原点在车辆后轮轴的中心，如下图所示：

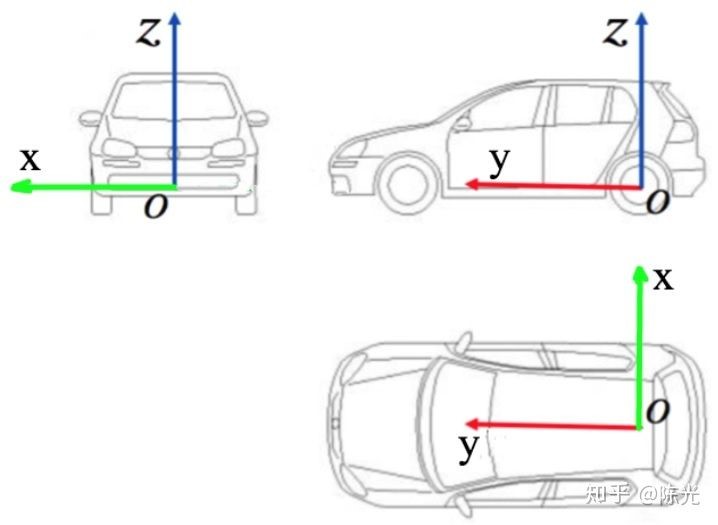
以安装在无人车左前方的角雷达（Corner radar）为例，角雷达的安装位置和坐标系如下图绿线所示：

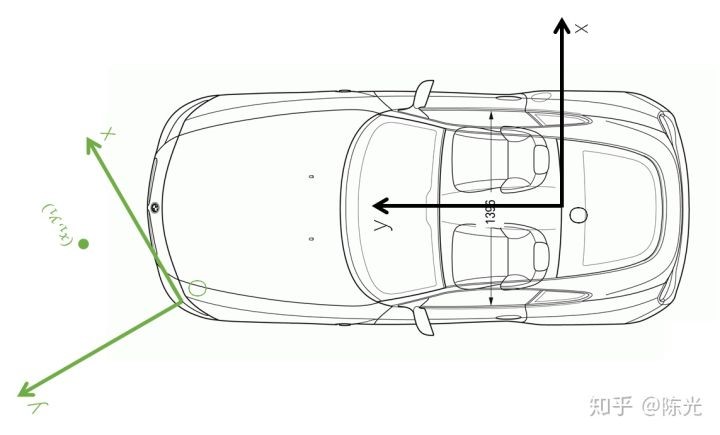
角雷达检测到的障碍物如图中的绿点所示，绿点在雷达坐标系下的坐标为$(x_1, y_1)$，为了便于理解暂不加入$z$方向的坐标，绿点转换到自车坐标系下需要经过一定的数学运算：

(1) 旋转
将角雷达坐标系沿着$z$轴进行一定角度的旋转，新坐标系与自车坐标系相平行，

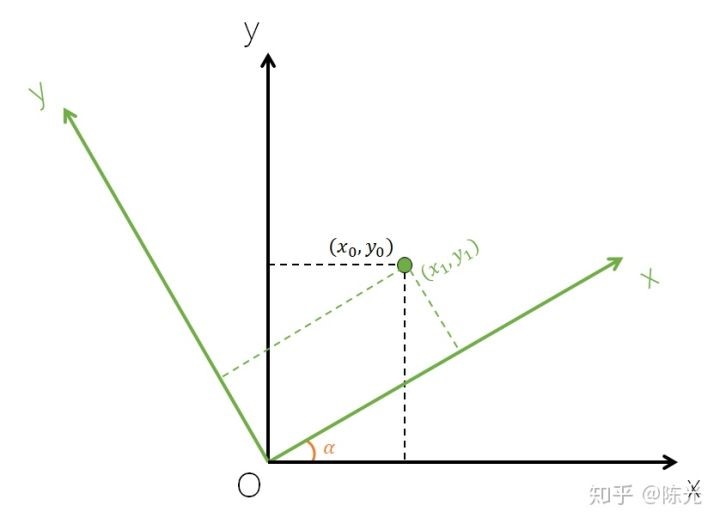
障碍物在角雷达坐标系下的坐标为$(x_1, y_1)$，假设障碍物在旋转后的新坐标系下的坐标为$(x_0, y_0)$，安装角度$α$（可测量），做辅助线后如下图所示：

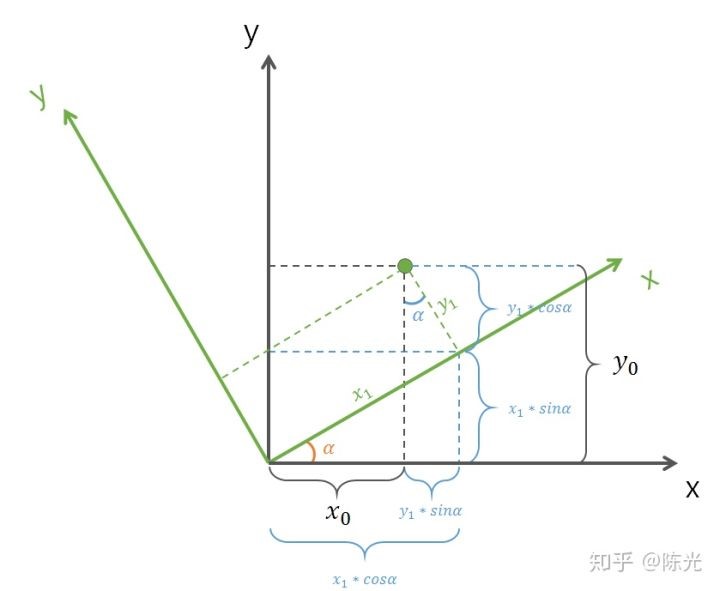
根据几何关系可得：

$$x_0=x_1*cosα-y_1*sinα \\ y_0=x_1*sinα+y_1*cosα$$

矩阵形式为：

$$\begin{bmatrix} x_0 \\ y_0 \end{bmatrix} =\begin{bmatrix} cosα & -sinα \\ sinα & cosα \end{bmatrix} *\begin{bmatrix} x_1 \\ y_1 \end{bmatrix}$$

由于旋转是绕$z$轴旋转，因此旋转前后$z$值保持不变，即$z_0$=$z_1$，故：

$$\begin{bmatrix} x_0 \\ y_0 \\ z_0 \end{bmatrix} =\begin{bmatrix} cosα & -sinα & 0 \\ sinα & cosα & 0 \\ 0 & 0 & 1 \end{bmatrix} *\begin{bmatrix} x_1 \\ y_1 \\ z_1 \end{bmatrix} =R_z *\begin{bmatrix} x_1 \\ y_1 \\ z_1 \end{bmatrix}$$

$R_z$为绕$z$轴的旋转矩阵，同样也有绕$x$轴的旋转矩阵$R_x$和绕$y$轴的旋转矩阵$R_y$，考虑到一般情况，上式变换为：

$$\begin{bmatrix} x_0 \\ y_0 \\ z_0 \end{bmatrix} =R_x*R_y*R_z *\begin{bmatrix} x_1 \\ y_1 \\ z_1 \end{bmatrix}$$

再加上一个平移矩阵，就能够得到障碍物在自车坐标系中的最终坐标描述：

$$\begin{bmatrix} x_0 \\ y_0 \\ z_0 \end{bmatrix} =R_x*R_y*R_z *\begin{bmatrix} x_1 \\ y_1 \\ z_1 \end{bmatrix} +T_{xyz}$$

以上过程也称为欧拉变换，但是欧拉变换会有一个不可避免的问题——万向锁，欧拉变换的过程中在某些特殊情况时，会导致少一个维度。为了解决欧拉变换存在的万向锁问题，引入了四元数的概念。四元数除了能够解决万向锁的问题外，还能在一定程度上简化计算，因而百度 Apollo 也选择了四元数作为各个传感器安装位置和角度的存储介质。

2 参考

1. 无人驾驶技术入门（十二）| 无人驾驶中的坐标转换

---