输出倒逼思考

0%

从贝叶斯滤波到无迹卡尔曼滤波

发表于
分类于 ， Valine：
无迹卡尔曼滤波基于无迹变换，无迹变换研究的是如何通过确定的采样点捕获经非线性变换的高斯随机变量的后验分布的问题。通过无迹变换得到相应的统计特性后，再结合标准卡尔曼滤波框架，便得到无迹卡尔曼滤波。标准无迹卡尔曼滤波的计算量与扩展卡尔曼滤波相当，但滤波精度要优于扩展卡尔曼滤波。

目录

目录-从贝叶斯滤波到无迹卡尔曼滤波

0 引言

在此前的文章《从贝叶斯滤波到扩展卡尔曼滤波》中，我们讲述了扩展卡尔曼滤波通过一阶泰勒级数展开将非线性高斯系统的状态转移函数 $f(x)$ 和（或）观测函数 $h(x)$ 线性化，然后采用标准卡尔曼滤波框架实现状态量的滤波过程。扩展卡尔曼滤波存在两方面的明显缺点：

  • 一阶泰勒级数展开忽略了二阶及以上的高阶项，因此精度一般（通常称为一阶精度），对于高度非线性问题效果较差；
  • 雅可比矩阵的计算较为繁琐，容易出错。

为解决强非线性条件下的状态估计问题，1995 年，S. J. Julier 和 J. K. Uhlmann 等人提出了无迹卡尔曼滤波（Unscented Kalman Filter，UKF）算法，并由 E. A. Wan 和 R. Vander Merwe 等人进一步完善。

无迹卡尔曼滤波基于无迹变换（Unscented Transform，UT），无迹变换研究的是如何通过确定的采样点捕获经非线性变换的高斯随机变量的后验分布的问题。通过无迹变换得到相应的统计特性后，再结合标准卡尔曼滤波框架，便得到无迹卡尔曼滤波。标准无迹卡尔曼滤波的计算量与扩展卡尔曼滤波相当，但滤波精度要优于扩展卡尔曼滤波。

1 无迹变换

1.1 什么是无迹变换

无迹变换的核心理念：

近似概率分布比近似任意的非线性函数或变换要相对容易。

无迹变换要解决的问题是：已知某随机变量（多维情形下是随机向量）的概率分布（均值和方差），求其经过某非线性函数 $g(·)$ 变换后的概率分布。基于上述思想，无迹变换的主要步骤为：

(1) 根据某种规则对随机变量的概率分布进行确定性采样，并为采样点分配权重（均值权重和方差权重），采样点我们通常称之为 sigma 点；

(2) 将每一个 sigma 点进行非线性变换，得到新的 sigma 点；

(3) 对非线性变换后的新的 sigma 点进行加权求和，分别计算加权均值和加权方差，用加权均值和加权方差近似表征随机变量经非线性变换后的概率分布。

如下图所示（《概率机器人》第 3.4 节 P49）：

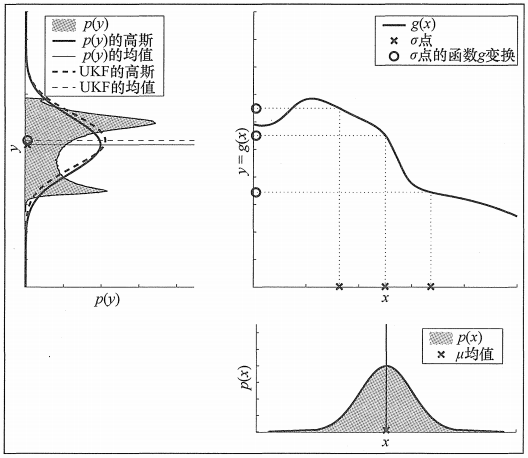
无迹变换示例

无迹卡尔曼滤波中使用的确定性采样方法是 sigma 点采样方法的一种具体实现，中心差分卡尔曼滤波（Central Difference Kalman Filter，CDKF）使用了 sigma 点采样方法的另一种具体实现，这类滤波算法我们统称为 sigma 点卡尔曼滤波（Sigma-Point Kalman Filter，SPKF）算法。

按照历史发展脉络来讲，无迹变换主要包括两种形式：一般形式的无迹变换和比例无迹变换（Scaled Unscented Transform，SUT）。两种无迹变换的区别主要体现在采样规则和权重计算上，下面将分别进行阐述。

1.2 一般形式的无迹变换

假设存在 $n$ 维随机向量 $X$，其服从均值 $\mu_x$ 和协方差 $\Sigma_x$ 的正态分布：

将 $X$ 经过非线性函数 $g(·)$ 进行变换，得到随机向量 $Y$，我们使用一般形式的无迹变换估计 $Y$ 的概率分布。一般形式的无迹变换最早由 Julier 等人提出，其主要操作流程如下所述：

步骤一：参数选择与权重计算

一般形式的无迹变换只涉及一个外部引入参数 $\kappa$，各 sigma 点（$2n+1$ 个）的权重分配如下：

其中，$\kappa \in \mathbb{R}$，表征了 sigma 点相对均值的散布程度，$\kappa$ 越大，非均值处的 sigma 点距离均值越远（参考步骤二），且所占权重越小，而均值处 sigma 点所占权重则相对越大。对于高斯问题，$n+\kappa = 3$ 是一个比较好的选择，对于非高斯问题（是的，无迹变换也适用于非高斯问题），$\kappa$ 应该选择其它更恰当的值。

步骤二：确定性采样

通常情况下，siama 点位于均值处及对称分布于主轴的协方差处（每维两个）。按照如下方法采样得到 $2n + 1$ 个 sigma 点，构成 $n \times (2n + 1)$ 的点集矩阵 $\mathcal{X}$：

其中，$(\sqrt{(n + \kappa)\Sigma_x})^{(i-1)}$ 表示矩阵 $(n + \kappa)\Sigma_x$ 作 Cholesky 分解后下三角矩阵的第 $i-1$ 列，$(\sqrt{(n + \kappa)\Sigma_x})^{(i-n-1)}$ 同理。

步骤三：sigma 点非线性变换

将每个 sigma 点（即 $\mathcal{X}$ 的每一列）进行 $g(·)$ 的非线性变换，得到变换后的新的点集矩阵 $\mathcal{Y}$：

步骤四：加权计算近似均值与近似协方差

1.3 比例无迹变换

从 1.2 节的内容中我们可以发现，当参数 $\kappa < 0$ 时，权重 $W^{(0)} = \frac{\kappa}{n+\kappa} < 0$，加权算得的近似协方差可能存在非半正定的情况。为应对该问题，Julier 等人后来提出无迹变换的改进形式——比例无迹变换，并由 Merwe 等人对其进行了简化。比例无迹变换与一般形式的无迹变换的主要区别体现在参数选取与 sigma 点权重计算上，其主要操作流程如下所述：

步骤一：参数选择与权重计算

比例无迹变换引入了四个外部参数：$\alpha$、$\beta$、$\kappa$ 和 $\lambda$，各 sigma 点（$2n+1$ 个）的权重分配如下：

其中，$W_m^{(i)}$ 表示计算近似均值时 sigma 点的权重，$W_c^{(i)}$ 表示计算近似协方差时 sigma 点的权重。参数 $\lambda$ 满足：

参数 $\alpha$ 和 $\kappa$ 为确定 sigma 点分布在均值多远的范围内的比例参数。$\alpha$ 满足 $10^{-4} \le \alpha \le 1$，为避免强非线性系统中的非局部效应问题，$\alpha$ 通常取一个较小值；$\kappa$ 满足 $\kappa \ge 0$，通常取 $\kappa = 3-n$ 或 $\kappa = 0$。

下图呈现了当 $\alpha$ 取值分别为 $0.3$ 和 $1$ 时，sigma 点的分布情况，从图中可以发现，$\alpha$ 取值越大，非均值处的 sigma 点距离均值越远。

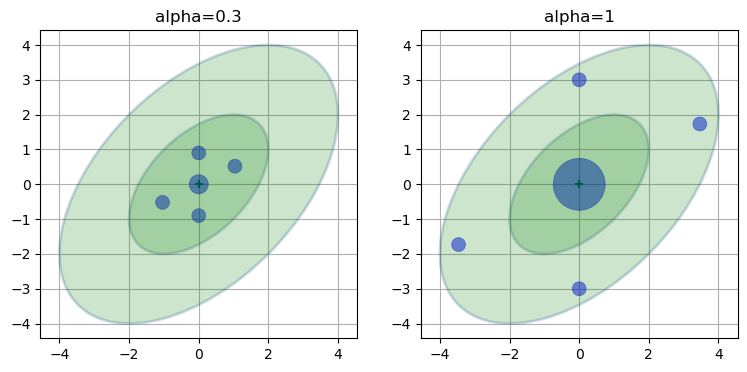
alpha 取不同值时 sigma 点的散布示例

参数 $\beta$ 用于引入随机变量概率分布的高阶矩信息，如果分布是精确的高斯分布，则 $\beta = 2$ 是最优选择。

步骤二：确定性采样

通常情况下，siama 点位于均值处及对称分布于主轴的协方差处（每维两个）。按照如下方法采样得到 $2n + 1$ 个 sigma 点，构成 $n \times (2n + 1)$ 的点集矩阵 $\mathcal{X}$：

其中，$(\sqrt{(n + \lambda)\Sigma_x})^{(i-1)}$ 表示矩阵 $(n + \lambda)\Sigma_x$ 作 Cholesky 分解后下三角矩阵的第 $i-1$ 列，$(\sqrt{(n + \lambda)\Sigma_x})^{(i-n-1)}$ 同理。

步骤三：sigma 点非线性变换

将每个 sigma 点（即 $\mathcal{X}$ 的每一列）进行 $g(·)$ 的非线性变换，得到变换后的新的点集矩阵 $\mathcal{Y}$：

步骤四：加权计算近似均值与近似协方差

2 无迹卡尔曼滤波的假设

无迹卡尔曼滤波与扩展卡尔曼滤波具有相同的前提假设。

2.1 与卡尔曼滤波相同的假设

(1) 假设一：状态量服从正态分布

(2) 假设二：观测量服从正态分布

(3) 假设三：过程噪声服从均值为 0 的正态分布

(4) 假设四：观测噪声服从均值为 0 的正态分布

2.2 与卡尔曼滤波不同的假设

(5) 假设五：状态转移函数和（或）观测函数为非线性函数

在卡尔曼滤波的前提假设中，认为状态方程中的状态转移函数 $f(x)$ 以及观测方程中的观测函数 $h(x)$ 均为线性函数。基于这种线性假设，存在常数或常矩阵 $F$，使得 $f(x)$ 可以写成卡尔曼滤波中的线性形式，存在常数或常矩阵 $H$，使得 $h(x)$ 也可以写成卡尔曼滤波中的线性形式。

不同于标准卡尔曼滤波，无迹卡尔曼滤波处理的是非线性高斯系统，假设系统的状态转移函数和（或）观测函数为非线性函数。

3 无迹卡尔曼滤波算法框架

根据噪声对系统的状态转移过程和观测过程的影响是线性可加的还是非线性不可加的，无迹卡尔曼滤波算法有两种形式：可加性噪声条件下的无迹卡尔曼滤波算法和非可加性噪声条件下的无迹卡尔曼滤波算法。

3.1 可加性噪声条件下的无迹卡尔曼滤波

在此前的文章《从概率到贝叶斯滤波》中，我们曾经这样描述系统的状态方程和观测方程：

从上式中我们可以发现，过程噪声 $Q_k$ 和观测噪声 $R_k$ 是以线性可加项的形式存在于系统状态方程和观测方程中的，这种形式的表述基于这样的前提假设：过程噪声 $Q_k$ 对系统状态转移过程的影响是线性的，观测噪声 $R_k$ 对系统观测过程的影响也是线性的。很明显，此种情况下，$Q_k$ 与 $X_k$ 是同维的，$R_k$ 与 $Y_k$ 是同维的。

由此引申出可加性噪声条件下的无迹卡尔曼滤波算法，《概率机器人》第 3.4 节 P53 对算法流程有着很好的描述。假设有如下已知条件：

  • 高斯的状态量随机向量 $X$，$n_X$ 维，记 $n_X = n$
  • $k - 1$ 时刻 $X$ 的后验均值与后验协方差：$\mu_{X_{k-1}}^+$，$\Sigma_{X_{k-1}}^+$
  • $k$ 时刻的外部控制量输入 $u_k$
  • 高斯的过程噪声随机向量：$Q\sim\mathcal{N}(0, \Sigma_Q)$
  • 状态转移函数：$f(X_{k-1}, u_k)$
  • 高斯的观测量随机向量 $Z$，$n_Z$ 维
  • $k$ 时刻 $Z$ 的观测取值 $z_k$
  • 高斯的观测噪声随机向量：$R\sim\mathcal{N}(0, \Sigma_R)$
  • 观测函数：$h(X_k)$

基于以上已知条件与符号定义，我们总结一下可加性噪声条件下的无迹卡尔曼滤波算法步骤（使用比例无迹变换）。

步骤一：初始化

初始化步骤需要做三件事：

选定滤波初值

根据观测量初值 $z_0$及观测函数 $h(·)$ 计算对应的状态量初始均值 $\mu_{X_0}^+$，设定状态量协方差初值 $\Sigma_{X_0}^+$。

选定无迹变换参数

设定比例无迹变换参数 $\alpha$、$\beta$、$\kappa$ 和 $\lambda$ 的参数值，若使用一般形式的无迹变换，仅需设定 $\kappa$ 的取值。

sigma 点权重计算

根据无迹变换参数取值及权重计算公式计算各 sigma 点权重。

对 $k = 1, 2, 3, ··· ,$ 执行：

步骤二：对 $k-1$ 时刻状态量 $X_{k-1}$ 的后验概率分布进行 sigma 采样

其中，$\gamma = \sqrt{(n + \lambda)}$。

步骤三：状态转移非线性变换

步骤四：加权计算 $k$ 时刻状态量 $X_k$ 的先验概率分布

由于过程噪声是线性可加的，所以此处 $\Sigma_Q$ 直接加在了加权协方差的末尾。

步骤五：对 $k$ 时刻状态量 $X_k$ 的先验概率分布进行 sigma 采样

某些时候，为降低运算量会省略此步，而在下一步骤中直接使用步骤三中的 sigma 点集 $\mathcal{X}_k^{-*(i)}$，这样做在一定程度上会降低精度。

步骤六：观测非线性变换

步骤七：加权计算 $k$ 时刻观测量 $Z_k$ 的概率分布

由于观测噪声是线性可加的，所以此处 $\Sigma_R$ 直接加在了加权协方差的末尾。

步骤八：计算状态量与观测量的互协方差

步骤九：计算卡尔曼增益

步骤十：计算 $k$ 时刻状态量 $X_k$ 的后验概率分布

步骤三、四构成了可加性噪声条件下的无迹卡尔曼滤波算法的预测步，步骤六、七、八、九、十则构成了更新步。可加性噪声条件下的无迹卡尔曼滤波算法流程可总结为：

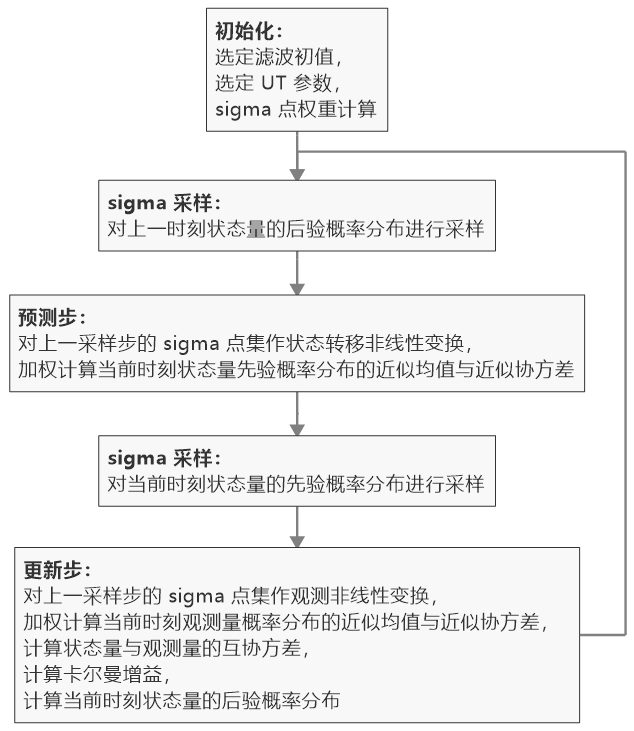
可加性噪声条件下的无迹卡尔曼滤波算法流程图

3.2 非可加性噪声条件下的无迹卡尔曼滤波

很多时候，噪声对系统的状态转移和观测的影响并非线性的，此种情况下，$Q_k$ 与 $X_k$ 不一定是同维的，$R_k$ 与 $Y_k$ 也不一定是同维的。此时，系统的状态方程和观测方程演变为：

过程噪声协方差和观测噪声协方差便不能像 3.1 节中描述的那样直接加在加权协方差的末尾。非可加性噪声条件下的无迹卡尔曼滤波算法的处理方法是对原始状态量作增广（augment）处理：

注意，上式中的 $\mathbf{0}$ 表示元素均为 $0$ 的块向量或块矩阵，故作了粗体显示，应与常值 $0$ 作区分。增广处理的方式并非只此一种，也可分步增广：在预测步开始前先对上一时刻状态量的后验概率分布作过程噪声增广，再在更新步开始前对当前时刻状态量的先验概率分布作观测噪声增广，《机器人学中的状态估计》一书中使用的便是分步增广的方式，两种增广处理方式实则是等效的。

记过程噪声随机向量 $Q$ 的维度为 $q$，观测噪声随机向量 $R$ 的维度为 $r$，增广状态量 $X_k^a$ 的维度为 $L = n + q + r$。下面我们基于 3.1 节中的已知条件和符号定义，阐述非可加性噪声条件下的无迹卡尔曼滤波算法的流程步骤。

步骤一：初始化

初始化步骤需要做三件事：

选定滤波初值

根据观测量初值 $z_0$及观测函数 $h(·)$ 计算对应的状态量初始均值 $\mu_{X_0}^+$，设定状态量协方差初值 $\Sigma_{X_0}^+$。

选定无迹变换参数

设定比例无迹变换参数 $\alpha$、$\beta$、$\kappa$ 和 $\lambda$ 的参数值，若使用一般形式的无迹变换，仅需设定 $\kappa$ 的取值。

sigma 点权重计算

根据无迹变换参数取值及权重计算公式计算各 sigma 点权重。

对 $k = 1, 2, 3, ··· ,$ 执行：

步骤二：对 $k-1$ 时刻状态量 $X_{k-1}$ 的后验概率分布进行增广处理

步骤三：对 $k-1$ 时刻状态量 $X_{k-1}$ 增广的后验概率分布进行 sigma 采样

其中，$\gamma = \sqrt{(L + \lambda)}$，且

  • $\mathcal{X}_{k-1}^{+a(i)}$ 我们读作 $k-1$ 时刻状态量增广的后验概率分布的 sigma 点集的第 $i$ 列。$\mathcal{X}_{k-1}^{+a}$ 的维度为 $L \times 2L$
  • $\mathcal{X}_{k-1}^{+aX(i)}$ 我们读作 $k-1$ 时刻状态量增广的后验概率分布的 sigma 点集的状态量分量的第 $i$ 列
  • $\mathcal{X}_{k-1}^{+aQ(i)}$ 我们读作 $k-1$ 时刻状态量增广的后验概率分布的 sigma 点集的过程噪声分量的第 $i$ 列
  • $\mathcal{X}_{k-1}^{+aR(i)}$ 我们读作 $k-1$ 时刻状态量增广的后验概率分布的 sigma 点集的观测噪声分量的第 $i$ 列

步骤四：状态转移非线性变换

$\mathcal{X}_k^-$ 表示 $k$ 时刻状态量先验概率分布的 sigma 点集，维度为 $n \times 2L$ （这一点需要注意）。再计算 $\mathcal{X}_k^-$ 时，我们只将 $\mathcal{X}_{k-1}^{+aX}$、$u_k$ 和 $\mathcal{X}_{k-1}^{+aQ}$ 传入了状态转移函数 $f(·)$，因为观测噪声对系统的状态转移过程无影响。

步骤五：加权计算 $k$ 时刻状态量 $X_k$ 的先验概率分布

很明显，步骤四中得到的 $\mathcal{X}_k^-$ 中已包含过程噪声信息，故此处在计算 $\Sigma_{X_k}^-$ 时并未像 3.1 节中那样在等式末尾添加了 $\Sigma_Q$ 项。

步骤六：观测非线性变换

正如步骤五中所说的，$\mathcal{X}_k^-$ 中已包含过程噪声信息，所以此处我们直接将 $\mathcal{X}_k^-$ 和 $\mathcal{X}_{k-1}^{+aR(i)}$ 传入了观测函数 $h(·)$ 来计算 $k$ 时刻观测量 $Z_k$ 的概率分布对应的 sigma 点集 $\mathcal{Z}_k$，而未像 3.1 节中那样对 $X_k$ 的先验概率分布进行了单独的采样。

步骤七：加权计算 $k$ 时刻观测量 $Z_k$ 的概率分布

很明显，步骤六中得到的 $\mathcal{Z}_k$ 中已包含观测噪声信息，故此处在计算 $\Sigma_{Z_k}$ 时并未像 3.1 节中那样在等式末尾添加了 $\Sigma_R$ 项。

步骤八：计算状态量与观测量的互协方差

步骤九：计算卡尔曼增益

步骤十：计算 $k$ 时刻状态量 $X_k$ 的后验概率分布

步骤四、五构成了非可加性噪声条件下的无迹卡尔曼滤波算法的预测步，步骤六、七、八、九、十则构成了更新步。非可加性噪声条件下的无迹卡尔曼滤波算法流程可总结为：

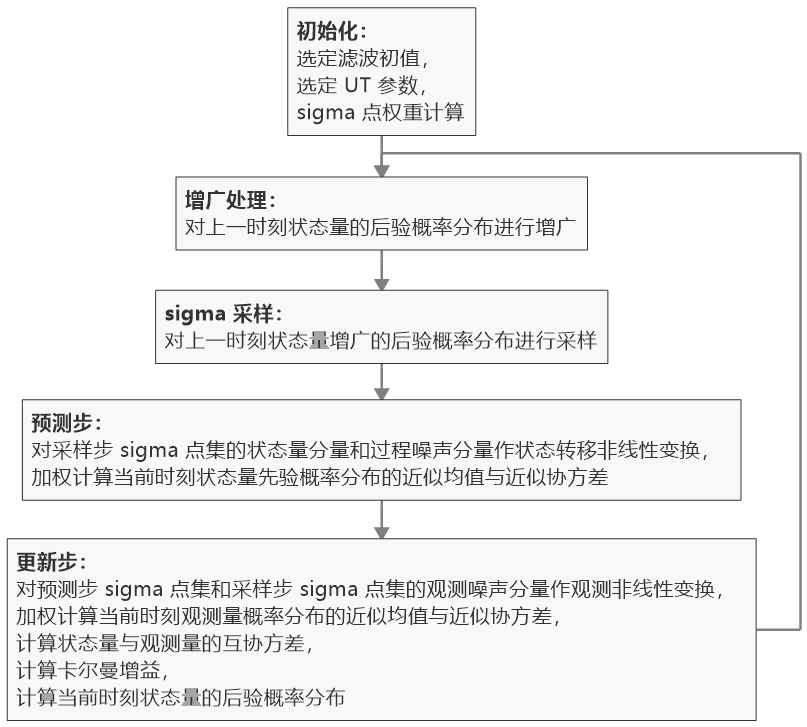
非可加性噪声条件下的无迹卡尔曼滤波算法流程图

在某些系统中，过程噪声和观测噪声可能其中一个对系统的影响是线性的（可加性噪声），而另一个对系统的影响是非线性的（非可加性噪声），这时需要结合 3.1 节与 3.2 节的方法来进行无迹卡尔曼滤波算法的设计，在下面的应用示例中你会看到具体是如何做的。

4 应用实例——基于毫米波雷达与无迹卡尔曼滤波的目标跟踪

4.1 系统分析

4.1.1 状态转移过程分析

在《从贝叶斯滤波到扩展卡尔曼滤波》中，我们讲解了毫米波雷达的检测原理，并基于扩展卡尔曼滤波算法实现了 CV 运动模型下的目标跟踪。此处，我们仍以毫米波雷达传感器为例，来讲解基于无迹卡尔曼滤波算法的目标跟踪过程。

不同的是，此次我们假设被跟踪目标近似地作匀速圆周运动，即运动模型为恒定转率和速度模型（Constant Turn Rate and Velocity，CTRV），如下图所示（图片来自 Udacity）。

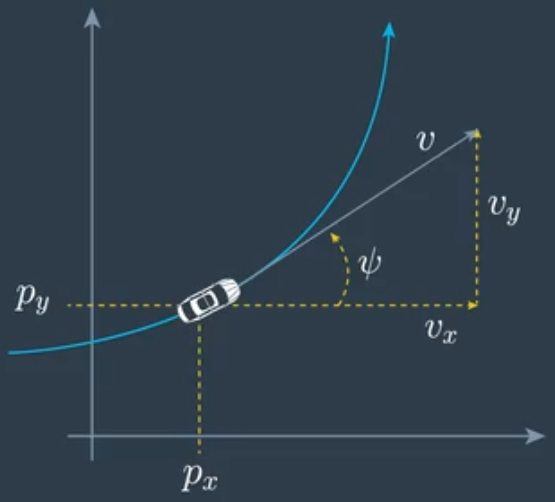
CTRV 运动模型示意图

在 CTRV 模型中，我们通常对目标在笛卡尔坐标系内的横坐标 $p_x$、纵坐标 $p_y$、线速率 $v$、航向角 $\psi$ 和航向角速率 $\omega$ 进行跟踪，其中 $\omega = \dot{\psi}$。状态量可设为：

我们先暂不考虑过程噪声的影响，则系统的状态方程（未计入噪声的）可表示为：

由换元法求复合函数定积分，容易得到：

故，求得系统的状态方程（未计入噪声的）为：

CTRV 是 CV 的一般形式，当 $\omega = 0$ 时，CTRV 便退化为 CV：

在上面的推导中，我们暂时忽略了过程噪声的干扰，但现实情况是，系统状态转移的过程中，目标的线速率 $v$ 和航向角速率 $\omega$ 并非一成不变，都存在微小扰动。假设 $v$ 受线加速度噪声 $q_a$ 的影响，$\omega$ 受角加速度噪声 $q_{\dot{\omega}}$ 的影响，$q_a$ 和 $q_{\dot{\omega}}$ 均为零均值的高斯白噪声：

则系统状态转移过程中总的过程噪声 $Q$ 可表示为：

$Q$ 的协方差 $\Sigma_Q$ 为：

$q_a$ 和 $q_{\dot{\omega}}$ 都对 $p_x$ 和 $p_y$ 存在影响，但此处我们忽略 $q_{\dot{\omega}}$ 对位移的影响，由运动学公式容易得到系统最终的状态方程：

4.1.2 观测过程分析

观测量仍然是毫米波雷达极坐标系下目标的径向距离 $\rho$、方向角 $\varphi$ 和径向距离变化率（径向速度）$\dot{\rho}$：

各观测量分量 $\rho$、$\varphi$、$\dot{\varphi}$ 对应的观测噪声分别为 $r_{\rho}$、$r_{\varphi}$、$r_{\dot{\varphi}}$，同样都是零均值的高斯白噪声：

则观测过程中总的观测噪声 $R$ 可表示为：

$R$ 的协方差 $\Sigma_R$ 为：

观测方程与《从贝叶斯滤波到扩展卡尔曼滤波》中相似，我们直接给出：

4.2 代码实现

从上面的分析中我们可以知道，过程噪声对系统的状态转移过程具有非线性影响，而观测噪声对系统的观测过程具有线性影响，因此需要结合 3.1 节与 3.2 节的内容进行无迹卡尔曼滤波算法的设计：

  • 实现 3.2 节的步骤二时，只需将过程噪声 $Q$ 增广到 $X_{k-1}$ 的后验概率分布
  • 实现 3.2 节的步骤六时，只需将预测步 sigma 点集 $\mathcal{X}_k^-$ 传入观测函数 $h(·)$
  • 实现 3.2 节的步骤七时，直接将观测噪声 $R$ 协方差 $\Sigma_R$ 添加至 $Z_k$ 协方差 $\Sigma_{Z_k}$ 的末尾

下面给出具体的 C++ 代码实现，为简便起见，实现过程中使用的无迹变换为一般形式的无迹变换，UT 参数只有 $\kappa$。代码框架比较清晰，完全遵循了 3.2 节的算法流程图，但没有去跑数据看仿真效果，工程实践中需要调节噪声协方差以及 UT 参数来获得较好的滤波结果。

UnscentedKalmanFilter.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#ifndef UNSCENTED_KALMAN_FILTER_
#define UNSCENTED_KALMAN_FILTER_

#include "Eigen/Dense"

class UnscentedKalmanFilter
{
private:
    bool is_inited;          // flag of initialization
    bool just_begin_filt;    // flag of just begining filt data
    uint64_t timestamp_last; // timestamp of last frame: us
    double dt;               // delta time: s

    int n_x;     // dimension of state vector X
    int n_x_aug; // dimension of augmented state vector X
    int n_z;     // dimension of measurement vector Z

    double std_a;         // standard deviation of longitudinal acceleration process noise: m/s^2
    double std_omega_dot; // standard deviation of yaw acceleration process noise: rad/s^2
    Eigen::MatrixXd Q;    // process noise covariance matrix

    double std_rho;     // standard deviation of range measurement noise: m
    double std_phi;     // standard deviation of bearing measurement noise: rad
    double std_rho_dot; // standard deviation of range rate measurement noise: m/s
    Eigen::MatrixXd R;  // measurement noise covariance matrix

    double kappa;            // unscented transform parameter κ
    Eigen::VectorXd weights; // weights vector of sigma points

    Eigen::VectorXd X;   // state vector
    Eigen::MatrixXd P_x; // state covariance matrix

    Eigen::VectorXd X_aug;         // augmented state vector
    Eigen::MatrixXd P_x_aug;       // augmented state covariance matrix
    Eigen::MatrixXd Sigmas_x_aug;  // sigma points of augmented posterior probability distribution of X(k-1)
    Eigen::MatrixXd Sigmas_x_pred; // sigma points of prior probability distribution of X(k)

    Eigen::MatrixXd Sigmas_z_pred; // sigma points of probability distribution of Z(k)

    Eigen::VectorXd Z;   // measurement vector
    Eigen::MatrixXd P_z; // measurement covariance matrix

    Eigen::MatrixXd P_xz; // cross covariance matrix of X and Z
    Eigen::MatrixXd K;    // kalman gain coefficient: K = P_xz * P_z.inverse()

public:
    Eigen::VectorXd Z_meas; // measurement value vector
    uint64_t timestamp_now; // timestamp of current frame: us

public:
    /**
     * @brief Construct a new Unscented Kalman Filter object
     *
     */
    UnscentedKalmanFilter();

    /**
     * @brief Destroy the Unscented Kalman Filter object
     *
     */
    ~UnscentedKalmanFilter();

    /**
     * @brief Return the initialization status of the ukf instance.
     *
     * @return bool
     */
    inline bool &IsInited() { return is_inited; }

    /**
     * @brief Reset the ukf instance.
     *
     */
    inline void Reset() { is_inited = false; }

    /**
     * @brief Normalize the input angle to [-PI, PI].
     *
     * @param angle
     */
    inline void NormalizeAngle(double &angle)
    {
        while (angle > M_PI)
            angle -= 2.0 * M_PI;
        while (angle < -M_PI)
            angle += 2.0 * M_PI;
    }

    /**
     * @brief To update measurement value vector and timestamp.
     *
     */
    inline void RecvRawData()
    {
        // Z_meas[0] = rho_new;
        // Z_meas[1] = phi_new;
        // Z_meas[2] = rho_dot_new;
        // timestamp_now = timestamp_new;

        dt = (timestamp_now - timestamp_last) / 1E6;
        timestamp_last = timestamp_now;
    }

    /**
     * @brief Initialization step.
     *
     */
    void Init();

    /**
     * @brief Augment posterior probability distribution of X(k-1).
     *
     */
    void AugmentLastPosteriorPDF();

    /**
     * @brief Sample the augmented posterior probability distribution of X(k-1).
     *
     */
    void SigmaSample();

    /**
     * @brief Prediction step.
     *
     */
    void Predict();

    /**
     * @brief Update step.
     *
     */
    void Update();
};

#endif

UnscentedKalmanFilter.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
#include "math.h"

#include "UnscentedKalmanFilter.h"

/**
 * @brief Construct a new Unscented Kalman Filter object
 *
 */
UnscentedKalmanFilter::UnscentedKalmanFilter()
    : is_inited(false),
      just_begin_filt(false),
      timestamp_last(0),
      dt(0.0),
      n_x(5),
      n_x_aug(7),
      n_z(3),
      std_a(1.5),         // need to be tuned according to the performance of the ukf
      std_omega_dot(0.8), // need to be tuned according to the performance of the ukf
      Q(2, 2),
      std_rho(0.3),
      std_phi(0.03),
      std_rho_dot(0.3),
      R(n_z, n_z),
      kappa(0.0),
      weights(2 * n_x_aug + 1),
      X(n_x),
      P_x(n_x, n_x),
      X_aug(n_x_aug),
      P_x_aug(n_x_aug, n_x_aug),
      Sigmas_x_aug(n_x_aug, 2 * n_x_aug + 1),
      Sigmas_x_pred(n_x, 2 * n_x_aug + 1),
      Sigmas_z_pred(n_z, 2 * n_x_aug + 1),
      Z(n_z),
      P_z(n_z, n_z),
      P_xz(n_x, n_z),
      K(n_x, n_z),
      Z_meas(n_z),
      timestamp_now(0)
{
}

/**
 * @brief Destroy the Unscented Kalman Filter object
 *
 */
UnscentedKalmanFilter::~UnscentedKalmanFilter() {}

/**
 * @brief Initialize the unscented kalman filter.
 *
 */
void UnscentedKalmanFilter::Init()
{
    if (!IsInited())
    {
        double rho = Z_meas(0);
        double phi = Z_meas(1);
        double rho_dot = Z_meas(2);

        double px = rho * cos(phi);
        double py = rho * sin(phi);

        // the initial value of X(2) confused me: 0, a small value or the initial
        // measurement value of rho_dot?
        X << px, py, 0.0, 0.0, 0.0;

        P_x << 1.0, 0.0, 0.0, 0.0, 0.0,
            0.0, 1.0, 0.0, 0.0, 0.0,
            0.0, 0.0, 1.0, 0.0, 0.0,
            0.0, 0.0, 0.0, 1.0, 0.0,
            0.0, 0.0, 0.0, 0.0, 1.0;

        Q << std_a * std_a, 0.0,
            0.0, std_omega_dot * std_omega_dot;

        R << std_rho * std_rho, 0.0, 0.0,
            0.0, std_phi * std_phi, 0.0,
            0.0, 0.0, std_rho_dot * std_rho_dot;

        kappa = 3 - n_x_aug;

        weights.fill(1 / (2 * (n_x_aug + kappa)));
        weights(0) = kappa / (n_x_aug + kappa);

        is_inited = true;
        just_begin_filt = true;
    }
    else
    {
        just_begin_filt = false;
    }
}

/**
 * @brief Augment posterior probability distribution of X(k-1).
 *
 */
void UnscentedKalmanFilter::AugmentLastPosteriorPDF()
{
    if (just_begin_filt)
        return;

    // augment mean
    X_aug.head(5) = X;
    X_aug(5) = 0.0;
    X_aug(6) = 0.0;

    // augment covariance
    P_x_aug.fill(0.0);
    P_x_aug.topLeftCorner(5, 5) = P_x;
    P_x_aug(5, 5) = Q(0, 0);
    P_x_aug(6, 6) = Q(1, 1);
}

/**
 * @brief Sample the augmented posterior probability distribution of X(k-1).
 *
 */
void UnscentedKalmanFilter::SigmaSample()
{
    if (just_begin_filt)
        return;

    double gamma = std::sqrt(n_x_aug + kappa);
    Eigen::MatrixXd chol_root = P_x_aug.llt().matrixL();

    Sigmas_x_aug.col(0) = X_aug;
    for (int i = 1; i < 2 * n_x_aug + 1; ++i)
    {
        if (i < n_x_aug + 1)
            Sigmas_x_aug.col(i) = X_aug + gamma * chol_root.col(i - 1);
        else
            Sigmas_x_aug.col(i) = X_aug - gamma * chol_root.col(i - n_x_aug - 1);
    }
}

/**
 * @brief Prediction step.
 *
 */
void UnscentedKalmanFilter::Predict()
{
    if (just_begin_filt)
        return;

    // predict sigma points of prior probability distribution of X(k)
    for (int i = 0; i < 2 * n_x_aug + 1; ++i)
    {
        double px = Sigmas_x_aug(0, i);
        double py = Sigmas_x_aug(1, i);
        double v = Sigmas_x_aug(2, i);
        double psi = Sigmas_x_aug(3, i);
        double omega = Sigmas_x_aug(4, i);
        double a = Sigmas_x_aug(5, i);
        double omega_dot = Sigmas_x_aug(6, i);

        Eigen::VectorXd state_trans_item_motion(n_x);
        Eigen::VectorXd state_trans_item_noise(n_x);

        state_trans_item_noise << 0.5 * a * cos(psi) * dt * dt,
            0.5 * a * sin(psi) * dt * dt,
            a * dt,
            0.5 * a * omega_dot * dt * dt,
            omega_dot * dt;

        if (std::fabs(omega_dot) > 0.001) // CTRV model
        {
            state_trans_item_motion << v / omega * (sin(psi + omega * dt) - sin(psi)),
                v / omega * (-cos(psi + omega * dt) + cos(psi)),
                0.0,
                omega * dt,
                0;
        }
        else // approximate CV model
        {
            state_trans_item_motion << v * cos(psi) * dt,
                v * sin(psi) * dt,
                0.0,
                omega * dt,
                0;
        }

        Sigmas_x_pred.col(i) = Sigmas_x_aug.head(5) + state_trans_item_motion + state_trans_item_noise;
    }

    // calculate approximate mean of prior PDF of X(k)
    X.fill(0.0);
    for (int i = 0; i < 2 * n_x_aug + 1; ++i)
        X += weights(i) * Sigmas_x_pred.col(i);

    // calculate approximate covariance of prior PDF of X(k)
    P_x.fill(0.0);
    for (int i = 0; i < 2 * n_x_aug + 1; ++i)
    {
        Eigen::VectorXd x_diff = Sigmas_x_pred.col(i) - X;
        NormalizeAngle(x_diff(3));

        P_x += weights(i) * x_diff * x_diff.transpose();
    }
}

/**
 * @brief Update step.
 *
 */
void UnscentedKalmanFilter::Update()
{
    if (just_begin_filt)
        return;

    // predict sigma points of probability distribution of Z(k)
    for (int i = 0; i < 2 * n_x_aug + 1; ++i)
    {
        double px = Sigmas_x_pred(0, i);
        double py = Sigmas_x_pred(1, i);
        double v = Sigmas_x_pred(2, i);
        double psi = Sigmas_x_pred(3, i);

        Sigmas_z_pred(0, i) = std::sqrt(px * px + py * py);
        Sigmas_z_pred(1, i) = atan2(py, px);
        Sigmas_z_pred(2, i) = (v * cos(psi) * px + v * sin(psi) * py) / Sigmas_z_pred(0, i);
    }

    // calculate approximate mean of PDF of Z(k)
    Z.fill(0.0);
    for (int i = 0; i < 2 * n_x_aug + 1; ++i)
        Z += weights(i) * Sigmas_z_pred.col(i);

    // calculate approximate covariance of PDF of Z(k)
    P_z.fill(0.0);
    for (int i = 0; i < 2 * n_x_aug + 1; ++i)
    {
        Eigen::VectorXd z_diff = Sigmas_z_pred.col(i) - Z;
        NormalizeAngle(z_diff(1));

        P_z += weights(i) * z_diff * z_diff.transpose();
    }
    P_z += R;

    // calculate cross covariance of X(k) and Z(k)
    P_xz.fill(0.0);
    for (int i = 0; i < 2 * n_x_aug + 1; ++i)
    {
        Eigen::VectorXd x_diff = Sigmas_x_pred.col(i) - X;
        NormalizeAngle(x_diff(3));

        Eigen::VectorXd z_diff = Sigmas_z_pred.col(i) - Z;
        NormalizeAngle(z_diff(1));

        P_xz += weights(i) * x_diff * z_diff.transpose();
    }

    // calculate kalman gain
    K = P_xz * P_z.inverse();

    // calculate mean of posterior PDF of X(k)
    Eigen::VectorXd z_diff = Z_meas - Z;
    NormalizeAngle(z_diff(1));
    X += K * z_diff;

    // calculate covariance of posterior PDF of X(k)
    P_x -= K * P_z * K.inverse();
}

main.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include "UnscentedKalmanFilter.h"

int main()
{
    UnscentedKalmanFilter ukf;

    while (true)
    {
        ukf.RecvRawData();

        ukf.Init();
        ukf.AugmentLastPosteriorPDF();
        ukf.SigmaSample();
        ukf.Predict();
        ukf.Update();
    }

    return 0;
}

点击这里下载完整工程。

5 总结

EKF 与 UKF 代表了处理非线性高斯问题的两种思路（UKF 同样适用于非线性非高斯系统）。EKF 利用一阶泰勒级数展开对非线性的状态转移函数 $f(·)$、观测函数 $h(·)$ 进行线性近似；而 UKF 利用确定性采样的方法对随机变量的概率密度函数进行近似。标准 UKF 的计算量与 EKF 相当，但滤波精度要优于 EKF。

参考

  1. A New Approach for Filtering Nonlinear Systems
  2. Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models
  3. A New Extension of the Kalman Filter to Nonlinear Systems
  4. The Scaled Unscented Transformation
  5. Kalman-and-Bayesian-Filters-in-Python
  6. FilterPy Documentation
  7. 《概率机器人》
  8. 《机器人学中的状态估计》
  9. 《最优状态估计——卡尔曼，$H_∞$ 及非线性滤波》
  10. 《卡尔曼滤波与组合导航原理》（第 3 版）
  11. EKF 与 UKF
  12. 扩展 Kalman 滤波(EKF)和无迹卡尔曼滤波(ukf)分析
  13. 无人驾驶汽车系统入门（三）——无损卡尔曼滤波，目标追踪，C++
  14. 无迹（损）卡尔曼滤波（UKF）理论讲解与实例
  15. P6_无损卡尔曼滤波器_udacity 无人驾驶
  16. 自动驾驶感知融合-无迹卡尔曼滤波(Lidar&Radar)
  17. CV,CA,CTRV 等运动模型，EKF，UKF 在运动模型下的分析与实践
猜你喜欢
Thank you for your donate!