输出倒逼思考

0%

从贝叶斯滤波到粒子滤波

发表于
分类于 ， Valine：
粒子滤波是贝叶斯滤波的一种非参数实现，所谓非参数，即不对滤波状态量的后验概率密度作任何假设。粒子滤波的主要思想是用一系列从后验得到的带权重的随机采样表示后验。从采样的角度考虑，粒子滤波与无迹卡尔曼滤波相似，区别在于，无迹卡尔曼滤波使用 sigma 确定性采样，通过无迹变换计算 sigma 样本点的位置与权重；而粒子滤波使用蒙特卡罗随机采样从建议分布中得到样本（粒子），并通过观测值更新粒子权重，针对粒子的权值退化问题，还涉及粒子的重采样步骤。粒子滤波算法广泛用于解决无人车的定位问题。

目录

目录-从贝叶斯滤波到粒子滤波

0 回顾与引言

在此前的文章《从概率到贝叶斯滤波》中，我们曾经提到，贝叶斯滤波框架下求解预测步中的先验概率密度函数 $f_{X_k}^-(x)$、更新步中的归一化常数 $\eta_k$、状态量最优估计 $\hat{x}_k$ 时均涉及到无穷积分，大多数情况无法得到解析解，使得贝叶斯滤波算法的直接应用十分困难。为了解决贝叶斯滤波积分难的问题，通常从两个角度出发：

(1) 作理想假设

  • 线性高斯
    假设状态转移函数 $g(x)$ 和观测函数 $h(x)$ 均为线性函数，过程噪声随机变量 $Q_k$ 和观测噪声随机变量 $R_k$ 均服从均值为 0 的正态分布。线性高斯问题可通过卡尔曼滤波（Kalman Filter）进行解决，详细内容请参考此前文章《从贝叶斯滤波到卡尔曼滤波》。

  • 非线性高斯
    假设状态转移函数 $g(x)$ 和（或）观测函数 $h(x)$ 为非线性函数，过程噪声随机变量 $Q_k$ 和观测噪声随机变量 $R_k$ 均服从均值为 0 的正态分布。非线性高斯问题可通过扩展卡尔曼滤波（Extended Kalman Filter）和无迹卡尔曼滤波（Unscented Kalman Filter）进行解决。扩展卡尔曼滤波通过一阶泰勒级数展开将非线性高斯系统的状态转移函数 $g(x)$ 和（或）观测函数 $h(x)$ 线性化，然后采用标准卡尔曼滤波框架实现状态量的滤波过程，详细内容请参考此前文章《从贝叶斯滤波到扩展卡尔曼滤波》；无迹卡尔曼滤波基于无迹变换，无迹变换研究的是如何通过确定的采样点捕获经非线性变换的高斯随机变量的后验分布的问题，通过无迹变换得到相应的统计特性后，再结合标准卡尔曼滤波框架，便得到无迹卡尔曼滤波，详细内容请参考此前文章《从贝叶斯滤波到无迹卡尔曼滤波》。

(2) 化连续为离散

对于强非线性非高斯问题，需要将无穷积分转化为离散的数值积分——即化整为零，由此可以引申出本文的主题——粒子滤波（Particle Filter，PF）。

粒子滤波是贝叶斯滤波的一种非参数实现，所谓非参数，即不对滤波状态量的后验概率密度作任何假设。粒子滤波的主要思想是用一系列从后验得到的带权重的随机采样表示后验。从采样的角度考虑，粒子滤波与无迹卡尔曼滤波相似，区别在于，无迹卡尔曼滤波使用 sigma 确定性采样，通过无迹变换计算 sigma 样本点的位置与权重；而粒子滤波使用蒙特卡罗随机采样从建议分布中得到样本（粒子），并通过观测值更新粒子权重，针对粒子的权值退化问题，还涉及粒子的重采样步骤。粒子滤波算法广泛用于解决无人车的定位问题。

关键词： 贝叶斯，大数定律，蒙特卡罗，重要性采样，序贯重要性采样，粒子退化，重采样，采样重要性重采样，无人车定位

1 蒙特卡罗方法

假设存在某一连续型随机变量 $X$，其概率密度函数为 $p(x)$，则 $X$ 的数学期望为：

若存在另一连续型随机变量 $Y$，满足 $Y = g(X)$，则 $Y$ 的数学期望为：

正如我们所知道的，上式中的 $\mathrm{E}(X)$ 和 $\mathrm{E}(Y)$ 可能很难得到解析解。蒙特卡罗（Monte Carlo）方法告诉我们，可以通过对随机变量的概率密度进行随机采样，并对样本进行加权求和来近似随机变量的期望，如此一来，积分问题便转化为有限样本点的求和问题。

假设 $\mathcal{X}$ 是从 $p(x)$ 中进行随机采样得到的样本集合，样本数量为 $N$，每一个样本（粒子）$\mathcal{X}^{(i)}$ 代表 $X$ 的一种可能状态，即

根据辛钦大数定律，$\mathcal{X}$ 的样本均值依概率 1 收敛于数学期望，即对 $\forall\epsilon > 0$，有

式 (1.4) 和 (1.5) 意味着，当样本数量 $N$ 足够大时，有

2 重要性采样

2.1 什么是重要性采样

如上述，如果我们能够对概率密度函数 $p(x)$ 进行随机采样，便可通过对样本进行加权求和来近似随机变量 $X$ 和 $Y=g(X)$ 的数学期望，然而现实情况是，$p(x)$ 可能很难直接采样，甚至根本无法采样。此时，可以选择从一个更加容易采样的概率密度函数 $q(x)$ 中进行随机采样得到样本集合 $\mathcal{X}$，并通过 $\mathcal{X}$ 近似估计 $\mathrm{E}(Y)$

其中

上述的采样方式称为重要性采样（Importance Sampling），其中的更易采样的概率密度函数 $q(x)$ 称为建议分布（Proposal Distribution），也称重要性密度（Importance Density）或重要性函数（Importance Function）。

令

显然

故，式 (2.1) 可改写为

我们记 $w^{(i)}=w(\mathcal{X}^{(i)})$，并记

$w^{(i)}$ 我们称之为粒子 $\mathcal{X}^{(i)}$ 的非归一化的重要性权重（Unnormalized Importance Weight），$\widetilde{w}^{(i)}$ 我们称之为归一化的重要性权重（Normalized Importance Weight），则式 (2.5) 等价于

从式 (2.7) 中我们不难发现，归一化的重要性权重 $\widetilde{w}^{(i)}$ 即对应粒子 $\mathcal{X}^{(i)}$ 的离散概率值（概率质量），只要得到了粒子 $\mathcal{X}^{(i)}$ 及其对应的归一化的重要性权重 $\widetilde{w}^{(i)}$，便可通过式 (2.7) 近似估计期望 $\mathrm{E}(Y)$。简言之，重要性采样要解决的是原分布难以采样甚至无法采样的问题。

2.2 序贯重要性采样

上述的重要性采样过程针对的是单一随机变量的估计，而对于贝叶斯估计而言，我们需要处理的是从 $0$ 时刻到 $k$ 时刻的随机过程

意即，我们需要估计的是条件期望

类似 2.1 节中的推导过程，我们从一个更加容易采样的概率密度函数 $q(x_{0:k}|z_{1:k})$ 中进行随机采样得到样本集合 $\mathcal{X}_{0:k}$，并通过 $\mathcal{X}_{0:k}$ 近似估计条件期望 $\mathrm{E}[g(X_k)|Z_{1:k}]$

其中

$\mathcal{X}_{0:k}^{(i)}$ 是由每一时刻的第 $i$ 个样本粒子依次增广构成的粒子簇

令

显然

故，式 (2.10) 可改写为

我们记 $w_k^{(i)}=w(\mathcal{X}_{0:k}^{(i)})$，并记

$w_k^{(i)}$ 我们称之为粒子簇 $\mathcal{X}_{0:k}^{(i)}$ 的非归一化的重要性权重，$\widetilde{w}^{(i)}$ 我们称之为归一化的重要性权重，则式 (2.15) 等价于

从式 (2.17) 中我们不难发现，归一化的重要性权重 $\widetilde{w}_k^{(i)}$ 即对应粒子簇 $\mathcal{X}_{0:k}^{(i)}$ 的离散概率值（概率质量），只要得到了粒子簇 $\mathcal{X}_{0:k}^{(i)}$ 及其对应的归一化的重要性权重 $\widetilde{w}_k^{(i)}$，便可通过式 (2.17) 近似估计条件期望 $\mathrm{E}[g(X_k)|Z_{1:k}]$。

式 (2.16) 中的重要性权重是批量形式，存在这样一个问题，每个新的时刻的观测数据到来时都需要重新批量计算整个状态序列的重要性权重，随着时间的推移，这无疑将带来巨大的资源消耗。为了递推地更新相邻时刻间粒子的重要性权重，我们引入序贯重要性采样（Sequential Importance Sampling，SIS）算法。

根据贝叶斯公式、马尔可夫状态独立性假设和马尔可夫观测独立性假设，我们很容易得到原分布的的递推形式

假定建议分布有如下的递推形式

将式 (2.18) 和式 (2.19) 代入式 (2.13)

根据式 (2.19) 对建议分布递推形式的假设，式 (2.11) 粒子簇的批量采样可以很自然地转化为单个粒子的序贯采样形式：

将式 (2.21) 代入式 (2.20) 便得到重要性权重的递推更新形式：

若我们只关心当前 $k$ 时刻状态的估计结果，则根据系统的马尔可夫特性，有

此时的建议分布只与 $k-1$ 时刻的状态 $x_{k-1}$ 和 $k$ 时刻的观测结果 $z_k$ 有关，这意味着，在实际应用时，我们无需存储更早时刻的历史状态序列和观测序列。根据式 (2.23)，式 (2.21) 演变为

将式 (2.23) 和式 (2.24) 代入式 (2.22)，可以得到重要性权重最终的递推更新形式

注意，式 (2.25) 中的 $w_k^{(i)}=w(\mathcal{X}_k^{(i)})$。按照式 (2.25) 递推地得到 $k$ 时刻每个粒子的重要性权重后，再对权重作归一化处理，最终便可根据式 (2.17) 近似估计条件期望。式 (2.24)、(2.25)、(2.16) 和 (2.17) 构成了 SIS 算法的核心流程，下面我们总结下 SIS 的整体框架伪代码。

简言之，序贯重要性采样是为了序贯地进行粒子采样，并递推地更新粒子的重要性权重。

3 粒子退化问题

3.1 概述

3.1.1 什么是粒子退化

SIS 算法在经历次多次迭代后，粒子重要性权重的方差可能将变得很大，从而引发粒子退化问题（Particle Degeneracy Problem）。所谓粒子退化，指的是大量粒子中只有少数粒子具有较高权重，而绝大多数粒子的权重都很小甚至接近于 $0$，导致计算加权均值时大量的运算资源被浪费在了小权重粒子上。粒子退化问题发生的根本原因是建议分布与真实分布的不匹配。

3.1.2 粒子退化程度的度量

为了度量粒子退化问题的严重程度，我们引入有效样本数 $N_{eff}$，并将其定义如下

$N_{eff}$ 的直接计算并不容易，我们通常代为使用其估计量 $\widehat{N_{eff}}$

$\widehat{N_{eff}}$ 越小，则意味着粒子退化越严重。抑制粒子退化问题最直观的方法是增加采样粒子数量 $N$，但这无疑会增加计算负担，降低算法实时性，以下两个手段则更具实操性：

  • 选择合适的建议分布
  • 在 SIS 算法流程结束后，实施粒子重采样（Resampling）步骤

3.2 建议分布的选择

最优的建议分布无疑就是真实的后验分布本身

但这个结论对于问题的求解并没有实际意义，因为正是由于后验分布未知或难于积分我们才引入了建议分布的概念。建议分布的设计已经发展出很多形式，并由此衍生出种类繁多的粒子滤波变种：

  • 以 UKF 生成建议分布的无迹粒子滤波（Unscented Particle Filter，UPF）
  • 以 EKF 生成建议分布的扩展卡尔曼粒子滤波（Extended Kalman Particle Filter，EKPF）
  • 通过构建辅助变量，提升和观测更为匹配的粒子被采样的概率的辅助粒子滤波（Auxiliary Particle Filter，APF）

UPF、EKPF、APF 等并不是本文的主题，这里我们介绍一种精度尚可，但实现更加简单的建议分布形式——先验状态转移概率分布。

根据式 (2.19) 和式 (2.23) 我们不难发现，只要条件建议分布 $q(x_k|x_{k-1},z_k)$ 一经确定，建议分布 $q(x_{0:k}|z_{1:k})$ 便自然确定，假设我们选取系统的先验状态转移概率分布 $p(x_k|x_{k-1})$ 作为条件建议分布

根据式 (3.4)，式 (2.24) 演变为

从式 (3.5) 我们可以知道，只要确定了系统先验的状态转移概率分布，便可以根据系统的状态转移方程进行粒子序贯采样。根据式 (3.4) 和式 (3.5)，式 (2.25) 演变为

从式 (3.6) 我们可以知道，只要完成了粒子的序贯采样，并确定了系统的似然概率分布，便可以根据系统的观测方程以及上一时刻粒子的重要性权重递推地更新当前时刻粒子的重要性权重（非归一化的）。

3.3 重采样

重采样也可有效抑制粒子退化问题。所谓重采样，指的是在得到当前时刻的粒子集及每个粒子归一化的重要性权重 $\{ \mathcal{X}_k^{(i)}, \widetilde{w}_k^{(i)} \}_{i=0}^{N-1}$ 后，根据每个粒子的权重需要进行重新采样，粒子权重越高，被重新采样到的概率也越高，这意味着，某些粒子在重采样后可能会被复制多份，而某些粒子在重采样后可能直接不存在了，如下图所示（参考 23，P263）。

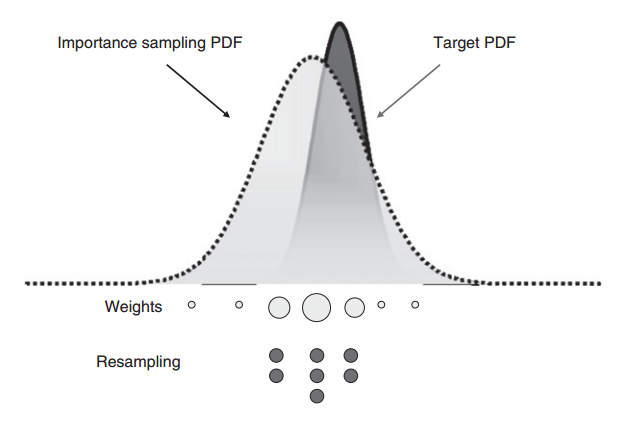
重采样示意图

重采样过程等价于对下面这个离散分布进行采样

我们记重采样得到的粒子集及每个粒子各自的权重为 $\{ \mathcal{X}_k^{\ast (j)}, w_k^{\ast (j)} \}_{j=0}^{N-1}$，因为是直接对离散分布进行采样，故

针对重采样过程，目前已发展出多种方法，如多项式重采样（Multinomial Resampling）、分层重采样（Stratified Resampling）、系统重采样（Systematic Resampling）、残差重采样（Residual Resampling）等，后面我们会对这几种方法作简单介绍并给出详尽的伪代码实现框架。

3.3.1 几种经典的重采样算法

3.3.1.1 多项式重采样

又称简单随机重采样（Simple Random Resampling）。其核心思想很简单，首先，计算粒子归一化权重的累积分布

然后，生成服从均匀分布 [0, 1] 内的随机数

使用二分搜索查找该随机数在累积分布中所处的位置，得到重采样粒子对应的原粒子的索引 $i$，$i$ 满足

多项式重采样算法的时间复杂度为 $\mathcal{O}(n\log(n))$，其中的对数项源于二分搜索的使用。下面我们给出多项式重采样的伪代码。

其中，$N$ 表示粒子总数，$N_r$ 表示重采样的粒子数（$N_r \leq N$。在单独使用多项式重采样时，$N_r=N$；在用于残差重采样的步骤二时，$N_r \lt N$），$\lfloor \cdot\rfloor$ 表示向下取整。在计算粒子权重的累积分布时，为避免圆整误差，需要令 $c_{N-1}=1$。此外，使用二分搜索时需要注意搜索区间的设置。

3.3.1.2 分层重采样

分层重采样将粒子归一化重要性权重的累积分布等分为 $N_r$ 层子区间，对每层子区间，使用一个介于子区间左右边界值的随机数来查找该层子区间重采样粒子所对应的原粒子索引，分层重采样算法的时间复杂度为 $\mathcal{O}(n)$。下面我们给出分层重采样的伪代码。

其中，$N$ 表示粒子总数，$N_r$ 表示重采样的粒子数（$N_r \leq N$。在单独使用分层重采样时，$N_r=N$；在用于残差重采样的步骤二时，$N_r \lt N$）。

3.3.1.3 系统重采样

系统重采样与分层重采样类似，唯一的区别在于，系统重采样中的每层子区间在查找各自重采样粒子对应的原粒子索引时使用的是同一个随机数，意即，系统重采样只涉及一次随机数生成操作，系统重采样算法的时间复杂度同样为 $\mathcal{O}(n)$。下面我们给出系统重采样的伪代码。

其中，$N$ 表示粒子总数，$N_r$ 表示重采样的粒子数（$N_r \leq N$。在单独使用系统重采样时，$N_r=N$；在用于残差重采样的步骤二时，$N_r \lt N$）。

3.3.1.4 残差重采样

残差重采样分两步进行：

步骤一：确定性拷贝采样

对原粒子集的每个粒子 $\mathcal{X}^{(i)}$ 根据 $N_{k_1}^{(i)}$ 作为复制次数进行拷贝采样，其中

例如，原粒子集共有 $N=1000$ 个粒子，第 $i=10$ 个粒子 $\mathcal{X}_k^{(10)}$ 的归一化的重要性权重为 $\widetilde{w}_k^{(10)}=0.0036$，则在残差重采样的步骤一中，$\mathcal{X}_k^{(10)}$ 将被拷贝 $N_{k_1}^{(10)}=\lfloor 1000*0.0036 \rfloor=3$ 次。在步骤一中，总的重采样粒子数为

每个拷贝后的重采样粒子的权重置为 $\frac{1}{N}$。

步骤二：残差随机采样

显然，由于忽略了 $N \widetilde{w}_k^{(i)}$ 的小数部分，经过步骤一后重采样粒子集中还缺少 $N_{k_2}=N-N_{k_1}^\ast$ 个粒子，对于剩余的待重采样的粒子，我们结合上面的重采样方法进行随机采样。首先，计算原粒子集中每个粒子经过确定性拷贝采样后新的归一化权重 $\widetilde{w}_k^{r(i)}$（这里我们称之为归一化的残差权重，上角标 $r$ 代表 residual）

然后，将 $\widetilde{w}_k^{r(i)}$ 和 $N_{k_2}$ 代入多项式重采样、分层重采样或系统重采样中的任意一种，完成剩余重采样粒子的采样。

下面我们给出残差重采样的伪代码，其中步骤二使用的是多项式重采样。

3.3.2 重采样的副作用

如果粒子的权值退化问题非常严重，那么重采样后的粒子将会是极少数个别粒子的大量副本，这意味粒子的多样性严重丧失，此时的粒子集已经无法很好地刻画原本的概率密度函数，我们称这种现象为粒子的样本贫化（Sample Impoverishment）。样本贫化极有可能导致滤波器发散，为了处理样本贫化问题，已经发展出很多方法，例如正则粒子滤波（Regularized Particle Filter，RPF），本文不对此作展开，有兴趣可以查阅相关文献。

3.3.3 基本的粒子滤波器

将 SIS 与重采样进行结合便构成了基本的粒子滤波器，下面我们总结下整体框架的伪代码（以 SIS + SystematicResampling 为例）。

其中，$N_{thr}$ 是用于决定是否执行重采样步骤的阈值，通常取 $N_{thr}=\frac{N}{2}$。

4 SIR 滤波器

这里我们介绍一种常用的经典粒子滤波算法实现——采样重要性重采样（Sampling Importance Resampling，SIR）滤波。

在 3.2 节的结论中我们已经知道，假设我们取系统的先验状态转移概率分布 $p(x_k|x_{k-1})$ 作为条件建议分布，便可以根据系统的状态转移方程进行粒子的序贯采样；同时，只要完成了粒子的序贯采样，并确定了系统的似然概率分布，便可以根据系统的观测方程以及上一时刻粒子的重要性权重递推地更新当前时刻粒子的重要性权重（非归一化的）。据此，我们对 3.3.3 节中的基本粒子滤波算法框架中的建议分布稍加修改，并在每次计算完归一化的重要性权重后都实施一次重采样，便可得到 SIR 滤波算法框架：

从框架中我们可以看出，SIR 的粒子序贯采样依赖上一时刻的粒子状态及系统的状态转移方程，我们称之为预测步；SIR 的粒子重要性权重序贯更新依赖上一时刻的粒子重要性权重及预测步粒子对应的似然概率，我们称之为更新步。预测步只改变粒子的位置，不改变粒子的权重；更新步只改变粒子的权重，不改变粒子的位置。 SIR 算法的流程示意图如下图所示（出自参考 24，P681）。

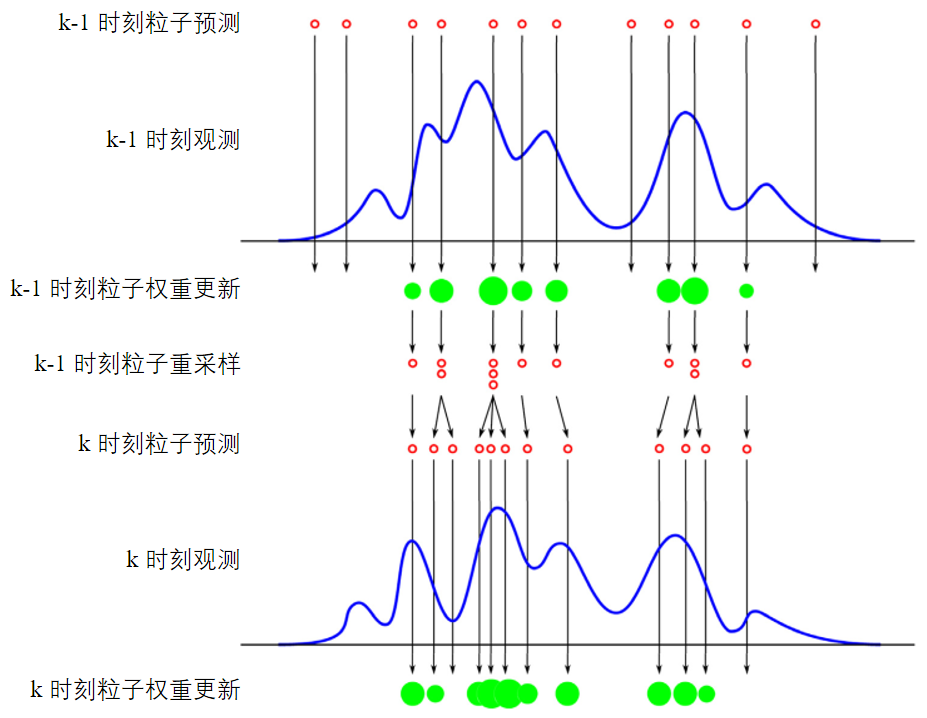
SIR 算法流程示意图

5 应用实例——基于粒子滤波的无人车定位

5.1 问题描述

粒子滤波常被用于解决无人车的定位问题。假设我们有一辆无人车，且已知下面的输入条件：

  • 无人车系统初始化瞬间的 GPS 输出（全局坐标系下的自车位置及航向），GPS 观测的不确定度（即位置与航向的标准差）
  • 每一时刻的外部控制输入（车速及航向角速率）
  • 一系列地图路标在全局坐标系下的位置及 id（假设 id 是从 $1$ 开始顺序排列的正整数）
  • 每一时刻若干个观测到的路标位置（自车坐标系），路标观测的不确定度
  • 用于路标感知的传感器有效测量范围

我们如何估计每个时刻无人车的定位信息（位置及航向）？这里我们使用粒子滤波，下图给出了基于粒子滤波的无人车定位流程（图片出自 Udacity）。

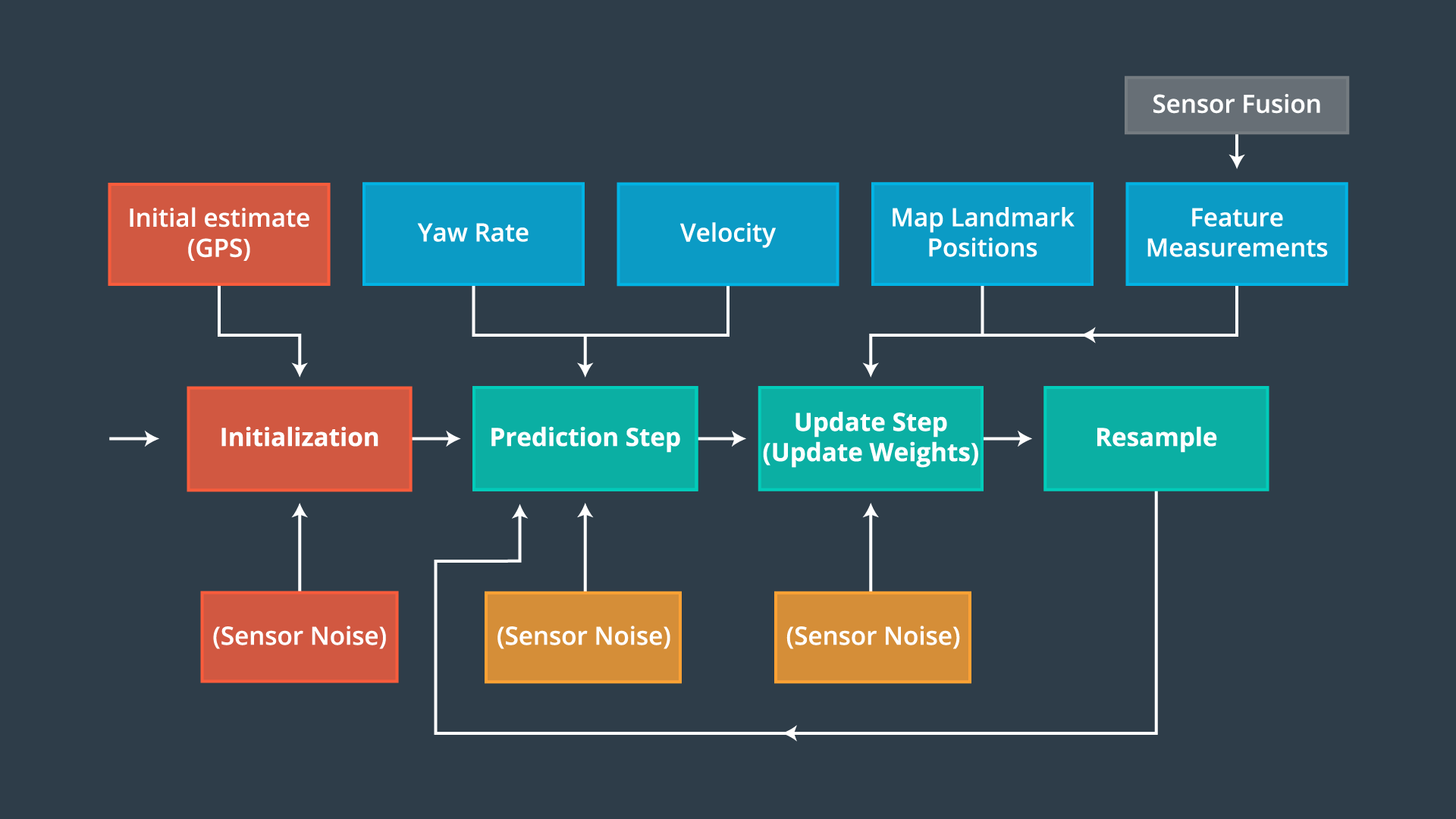
基于粒子滤波的无人车定位流程示意图

下面我们结合 SIR 算法框架及具体代码来详细阐述，代码实现基于 Udacity 的工程框架并进行了优化重构，点击这里查看 Udacity 源码。这里我们只关注核心算法本身，因此没有做仿真环节，相比理论分析，经典粒子滤波的代码实现要简单得多，实际效果在工程开发中去调试体会即可。

5.2 代码实现

5.2.1 初始化

我们假设 GPS 的位置及航向输出服从正态分布，因此在得到 GPS 的初始输出后，我们可以根据初始值（均值 $\mu$）和 GPS 观测不确定度（标准差 $\sigma$）构造无人车的定位初始分布，并通过对初始分布进行随机采样完成粒子集的初始化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * @brief Initialize the particle filter.
 *
 * @param x Initial x position [m] from GPS.
 * @param y Initial y position [m] from GPS.
 * @param theta Initial heading angle [rad] from GPS.
 * @param std_pos Array of dimension 3 [standard deviation of x [m],
 *   standard deviation of y [m], standard deviation of theta [rad]]
 */
void ParticleFilter::Init(const double &x, const double &y, const double &theta,
                          const double std_pos[])
{
    if (!IsInited())
    {
        // create normal distributions around the initial gps measurement values
        std::default_random_engine gen;
        std::normal_distribution<double> norm_dist_x(x, std_pos[0]);
        std::normal_distribution<double> norm_dist_y(y, std_pos[1]);
        std::normal_distribution<double> norm_dist_theta(theta, std_pos[2]);

        // initialize particles one by one
        for (size_t i = 0; i < n_p; ++i)
        {
            particles(0, i) = norm_dist_x(gen);
            particles(1, i) = norm_dist_y(gen);
            particles(2, i) = norm_dist_theta(gen);
        }

        // initialize weights to 1 / n_p
        weights_nonnormalized.fill(1 / n_p);
        weights_normalized.fill(1 / n_p);

        is_inited = true;
    }
}

有几点说明如下：

  • 这里使用了 C++ 的随机数引擎 std::default_random_engine 和正态分布模板类 std::normal_distribution 实现了高斯随机数的生成
  • particles 是 $3\times n_p$ 的粒子 Eigen 矩阵，$n_p$ 表示粒子数目，我们在构造函数的初始值列表中将其初始化为了 $1000$，矩阵的每一列表示一个粒子的状态，矩阵的第 $0$、$1$、$2$ 行分别表示粒子的横向位置 $x$、纵向位置 $y$ 和航向角 $\theta$
  • weights_nonnormalized 和 weights_normalized 分别表示未归一化和归一化的重要性权重，数据类型都是 $n_p\times 1$ 的 Eigen 向量。很多粒子滤波教程中使用同一个变量存放未归一化和归一化的重要性权重，这样也是可以的，这里我们的目的是使代码逻辑更加清晰。

5.2.2 预测

在预测步中，我们需要根据无人车的运动模型、车速、航向角速率、相邻两帧的时间间隔等将上一步的粒子集向当前时刻进行预测。这里我们我们假设自车遵从 CRTV 运动模型，关于 CRTV，在此前文章《从贝叶斯滤波到无迹卡尔曼滤波》中我们已经介绍过，不再赘述，这里我们这里直接给出不计噪声时的 CRTV 状态方程

式 (5.1) 中，$\omega$ 即自车的航向角速率。CTRV 是 CV 的一般形式，当 $\omega = 0$ 时，CTRV 退化为 CV。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
 * @brief Predict new state of particle according to the system motion model.
 *
 * @param velocity Velocity of car [m/s]
 * @param yaw_rate Yaw rate of car [rad/s]
 * @param delta_t delta time between last timestamp and current timestamp [s]
 * @param std_pos Array of dimension 3 [standard deviation of x [m],
 *   standard deviation of y [m], standard deviation of yaw [rad]]
 */
void ParticleFilter::Predict(const double &velocity, const double &yaw_rate,
                             const double &delta_t, const double std_pos[])
{
    if (!IsInited())
        return;

    // create process noise's normal distributions of which the mean is zero
    std::default_random_engine gen;
    std::normal_distribution<double> norm_dist_x(0, std_pos[0]);
    std::normal_distribution<double> norm_dist_y(0, std_pos[1]);
    std::normal_distribution<double> norm_dist_theta(0, std_pos[2]);

    // predict state of particles one by one
    for (size_t i = 0; i < n_p; ++i)
    {
        double theta_last = particles(2, i);

        Eigen::Vector3d state_trans_item_motion;
        Eigen::Vector3d state_trans_item_noise;

        state_trans_item_noise << norm_dist_x(gen), norm_dist_y(gen), norm_dist_theta(gen);

        if (std::fabs(yaw_rate) > 0.001) // CTRV model
        {
            state_trans_item_motion << velocity / yaw_rate * (sin(theta_last + yaw_rate * delta_t) - sin(theta_last)),
                velocity / yaw_rate * (-cos(theta_last + yaw_rate * delta_t) + cos(theta_last)),
                yaw_rate * delta_t;
        }
        else // approximate CV model
        {
            state_trans_item_motion << velocity * cos(theta_last) * delta_t,
                velocity * sin(theta_last) * delta_t,
                yaw_rate * delta_t;
        }

        // predict new state of the ith particle
        particles.col(i) = particles.col(i) + state_trans_item_motion + state_trans_item_noise;

        // normalize theta
        NormalizeAngle(particles(2, i));
    }
}

状态转移过程中的过程噪声我们假设为零均值的高斯白噪声。很明显预测步只改变了每个粒子的状态，未改变粒子的权重。每个粒子的预测航向角我们都做了 $[-\pi, \pi]$ 的归一化处理，后面在计算系统最终的加权状态估计时不需要重复处理。

5.2.3 更新

更新步的目的是根据最新的路标观测结果（自车局部坐标系下的横纵向相对位置），更新预测步后每个粒子的重要性权重。更新步主要由以下四个子步骤组成，需要对粒子集中的每个粒子依次执行以下步骤，我们结合代码进行阐述。

步骤 (1)： 坐标变换

无人车实时观测到的路标结果基于自车局部坐标系，我们将其转换到地图的全局坐标系，关于坐标系变换推导并不复杂，可见参考 34。假设当前时刻自车观测到某个路标 $lmrk(x_c, y_c)$，下角标 $c$ 表示自车坐标系，该路标对应于地图坐标系中的位置为 $lmrk(x_m, y_m)$，下角标 $m$ 表示地图坐标系。对于粒子 $p(x_p, y_p, \theta_p)$，下角标 $p$ 表示粒子，我们直接给出从 $lmrk(x_c, y_c)$ 到 $lmrk(x_m, y_m)$ 的坐标变换方程。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @brief Transform observed landmarks from local ego vehicle coordinate to
 *   global map coordinate.
 *
 * @param lmrks_obs Observed landmarks in ego vehicle coordinate.
 * @param particle Single particle with state of [x, y, theta]
 * @param lmrks_trans2map Observed landmarks transformed from local ego vehicle
 *   coordinate to global map coordinate.
 */
void ParticleFilter::TransLandmarksFromVehicle2Map(const std::vector<LandMark_Obs> &lmrks_obs,
                                                   const Eigen::Vector3d &particle,
                                                   std::vector<LandMark_Map> &lmrks_trans2map)
{
    for (size_t i = 0; i < lmrks_obs.size(); ++i)
    {
        lmrks_trans2map[i].x = lmrks_obs[i].x * cos(particle(2)) -
                               lmrks_obs[i].y * sin(particle(2)) + particle(0);

        lmrks_trans2map[i].y = lmrks_obs[i].x * sin(particle(2)) +
                               lmrks_obs[i].y * cos(particle(2)) + particle(1);
    }
}

步骤 (2)： 查找传感器感知范围内的地图路标

传感器的实际感知范围是有限的，我们需要找到每个粒子对应的传感器感知范围内的地图路标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * @brief Find map landmarks within the sensor measuremet range.
 *
 * @param lmrks_map All map landmarks.
 * @param particle Single particle with state of [x, y, theta]
 * @param snsr_range Sensor measuremet range.
 * @param lmrks_within_range Map landmarks within the sensor measuremet range.
 */
void ParticleFilter::FindMapLandmarksWithinSensorRange(const std::vector<LandMark_Map> &lmrks_map,
                                                       const Eigen::Vector3d &particle,
                                                       const double &snsr_range,
                                                       std::vector<LandMark_Map> &lmrks_within_range)
{
    static double distance_threshold_square = snsr_range * snsr_range;

    for (auto landmark : lmrks_map)
    {
        double distance_square = std::pow(particle(0) - landmark.x, 2) +
                                 std::pow(particle(1) - landmark.y, 2);

        if (distance_square <= distance_threshold_square)
            lmrks_within_range.push_back(landmark);
    }
}

步骤 (1) 和步骤 (2) 作为步骤 (3) 的输入，其顺序无关紧要。

步骤 (3)： 数据关联

数据关联的目的是找到观测路标与实际地图路标的一一对应关系，步骤 (4) 中需要通过这个对应关系更新每个粒子的权重。这里我们使用一种最为简单的数据关联方法——最近邻（Nearest Neighbor，NN）数据关联，其核心思想很直观：对于两个待关联的数据集，数据间的欧氏距离越小，关联的概率越高。NN 数据关联方法的优缺点总结如下（图片出自 Udacity）。

最近邻数据关联的优缺点

下面我们给出基于 NN 的数据关联 C++ 实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * @brief Associate observed landmarks which have been transformed to global
 *   map coordinate with map landmarks within the sensor measuremet range.
 *
 * @param lmrks_within_range Map landmarks within the sensor measuremet range.
 * @param lmrks_trans2map Observed landmarks transformed from local ego vehicle
 *   coordinate to global map coordinate.
 */
void ParticleFilter::DataAssociation(const std::vector<LandMark_Map> &lmrks_within_range,
                                     std::vector<LandMark_Map> &lmrks_trans2map)
{
    for (auto &landmark_trans2map : lmrks_trans2map)
    {
        double distance_min = std::numeric_limits<double>::max();

        for (auto &landmark_within_range : lmrks_within_range)
        {
            double distance_square = std::pow(landmark_trans2map.x - landmark_within_range.x, 2) +
                                     std::pow(landmark_trans2map.y - landmark_within_range.y, 2);

            if (distance_square < distance_min)
            {
                distance_min = distance_square;
                landmark_trans2map.id = landmark_within_range.id;
            }
        }
    }
}

关于数据关联匹配，还有很多其它优秀算法，后面会单独开几篇文章进行介绍。

步骤 (4)： 粒子权重更新

执行完关联步后，每个观测路标都对应一个地图路标，我们需要根据每个观测路标与地图路标的关联匹配程度来计算粒子的似然概率。这里我们假设对每个路标的观测都服从二元高斯分布，且相互独立，观测噪声也是高斯的，则每个观测路标的似然概率密度为

其中，$x$ 和 $y$ 分别表示观测路标转换到地图坐标系后的横向位置和纵向位置，$\mu_x$ 和 $\mu_y$ 分别表示观测路标关联上的地图路标的横向位置和纵向位置， $\sigma_x$ 和 $\sigma_y$ 表示路标观测的标准差。由于对每个路标的观测相互独立，粒子的总的似然概率密度为

其中，$m$ 表示观测路标的数量。将每个观测路标转换到地图坐标系后的测量值代入式 (5.4) 便可得到粒子总的似然概率，结合粒子上一时刻的权重便可近似地序贯更新粒子当前时刻的权重（未归一化的）。下面我们给出权重更新部分的 C++ 实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * @brief For each observed landmark with an associated landmark, calculate
 *   its' weight contribution, and then multiply to particle's final weight.
 *
 * @param lmrks_trans2map Observed landmarks transformed from local ego vehicle
 *   coordinate to global map coordinate.
 * @param lmrks_map All map landmarks.
 * @param std_lmrks Array of dimension 2 [Landmark measurement uncertainty
 *   [x [m], y [m]]]
 * @param weight Non-normalized weight of particle.
 */
void ParticleFilter::UpdateWeight(const std::vector<LandMark_Map> &lmrks_trans2map,
                                  const std::vector<LandMark_Map> &lmrks_map,
                                  const double std_lmrks[],
                                  double &weight)
{
    double likelyhood_probability_particle = 1.0;
    double sigma_x = std_lmrks[0];
    double sigma_y = std_lmrks[1];

    for (auto &landmark_trans2map : lmrks_trans2map)
    {
        double x = landmark_trans2map.x;
        double y = landmark_trans2map.y;
        double ux = lmrks_map.at(landmark_trans2map.id - 1).x;
        double uy = lmrks_map.at(landmark_trans2map.id - 1).y;
        double exponent = -(std::pow(x - ux, 2) / (2 * std::pow(sigma_x, 2)) +
                            std::pow(y - uy, 2) / (2 * std::pow(sigma_y, 2)));
        double likelyhood_probability_landmark = 1.0 / (2 * M_PI * sigma_x * sigma_y) *
                                                 std::exp(exponent);
        likelyhood_probability_particle *= likelyhood_probability_landmark;
    }

    weight *= likelyhood_probability_particle;
}

下面是整个更新步的代码实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * @brief
 *
 * @param lmrks_obs Observed landmarks in local ego vehicle coordinate.
 * @param snsr_range Sensor measuremet range.
 * @param lmrks_map All map landmarks.
 * @param std_lmrks Array of dimension 2 [Landmark measurement uncertainty
 *   [x [m], y [m]]]
 */
void ParticleFilter::Update(const std::vector<LandMark_Ego> &lmrks_obs,
                            const double &snsr_range,
                            const std::vector<LandMark_Map> &lmrks_map,
                            const double std_lmrks[])
{
    // process particles one by one
    for (size_t i = 0; i < n_p; ++i)
    {
        // step1: transform observed landmarks from local ego vehicle coordinate
        // to global map coordinate
        std::vector<LandMark_Map> landmarks_trans2map(lmrks_obs.size());
        TransLandmarksFromVehicle2Map(lmrks_obs, particles.col(i), landmarks_trans2map);

        // step2: find map landmarks within the sensor measuremet range
        std::vector<LandMark_Map> landmarks_within_sensor_range;
        FindMapLandmarksWithinSensorRange(lmrks_map, particles.col(i), snsr_range,
                                          landmarks_within_sensor_range);

        // step3: associate observed landmarks which have been transformed to
        // global map coordinate with map landmarks within the sensor measuremet
        // range
        DataAssociation(landmarks_within_sensor_range, landmarks_trans2map);

        // step4: for each observed landmark with an associated landmark, calculate
        // its' weight contribution, and then multiply to particle's final weight
        UpdateWeight(landmarks_trans2map, lmrks_map, std_lmrks, weights_nonnormalized(i));
    }
}

很明显更新步只改变了每个粒子的权重，未改变粒子的状态。

5.2.4 粒子权重归一化

完成粒子非归一化权重的更新后，我们需要计算粒子新的归一化的权重，作为后面重采样步骤的输入。

1
2
3
4
5
6
7
8
9
10
11
/**
 * @brief Normalize the weights of particles.
 *
 * @param w_nonnormalized Weights to be normalized.
 * @param w_normalized Weights which have been normalized.
 */
inline void NormalizeWeights(const Eigen::VectorXd &w_nonnormalized,
                             Eigen::VectorXd &w_normalized)
{
    w_normalized = w_nonnormalized / w_nonnormalized.sum();
}

5.2.5 重采样

完成粒子权重归一化后，我们需要对粒子集进行重采样。对于重采样步骤，大多数基于 Udacity 工程框架的开源项目使用了 C++ 标准库中的离散分布模板类 std::discrete_distribution ，这里我们“舍近求远”，手工实现 3.3.1 节中介绍的四种重采样算法，以加深对重采样的理解，随机数的生成我们通过模板类 std::uniform_real_distribution 实现。

多项式重采样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * @brief Multinomial resampling method.
 *
 * @param particles_ori Particles before resampling.
 * @param weights_ori_norm Normalized weights before resampling.
 * @param particles_resampled Particles after resampling.
 * @param weights_resampled Weights after resampling.
 * @param N_r Number of particles to resample.
 */
void ParticleFilter::MultinomialResampling(const Eigen::MatrixXd &particles_ori,
                                           const Eigen::VectorXd &weights_ori_norm,
                                           Eigen::MatrixXd &particles_resampled,
                                           Eigen::VectorXd &weights_resampled,
                                           uint32_t N_r)
{
    uint32_t N = weights_ori_norm.size();
    uint32_t left, right, middle;

    Eigen::VectorXd weights_cum_sum = CalcWeightsCumSum(weights_ori_norm);

    for (size_t j = N - N_r; j < N; ++j)
    {
        // produces random values u, uniformly distributed on the interval [0.0, 1.0)
        std::random_device rd;
        std::mt19937 gen(rd());
        std::uniform_real_distribution<> uniform_dist(0.0, 1.0);
        double u = uniform_dist(gen);

        // select the resampled particle using binary search
        left = 0;
        right = N - 1;
        while (left < right)
        {
            middle = std::floor((left + right) / 2);
            if (u > weights_cum_sum(middle))
                left = middle + 1;
            else
                right = middle;
        }

        particles_resampled(j) = particles_ori(right);
        weights_resampled(j) = 1 / N;
    }
}

分层重采样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * @brief Stratified resampling method.
 *
 * @param particles_ori Particles before resampling.
 * @param weights_ori_norm Normalized weights before resampling.
 * @param particles_resampled Particles after resampling.
 * @param weights_resampled Weights after resampling.
 * @param N_r Number of particles to resample.
 */
void ParticleFilter::StratifiedResampling(const Eigen::MatrixXd &particles_ori,
                                          const Eigen::VectorXd &weights_ori_norm,
                                          Eigen::MatrixXd &particles_resampled,
                                          Eigen::VectorXd &weights_resampled,
                                          uint32_t N_r)
{
    uint32_t N = weights_ori_norm.size();

    Eigen::VectorXd weights_cum_sum = CalcWeightsCumSum(weights_ori_norm);

    uint32_t i = 0;

    for (size_t j = N - N_r; j < N; ++j)
    {
        // produces random values u0, uniformly distributed on the interval [0.0, 1.0 / N_r)
        // then calculate u = u0 + (j - (N - N_r)) / N_r
        std::random_device rd;
        std::mt19937 gen(rd());
        std::uniform_real_distribution<> uniform_dist(0.0, 1 / N_r);
        double u0 = uniform_dist(gen);
        double u = u0 + (j - (N - N_r)) / N_r;

        // select the resampled particle
        while (weights_cum_sum(i) < u)
            ++i;

        particles_resampled(j) = particles_ori(i);
        weights_resampled(j) = 1 / N;
    }
}

系统重采样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * @brief Systematic resampling method.
 *
 * @param particles_ori Particles before resampling.
 * @param weights_ori_norm Normalized weights before resampling.
 * @param particles_resampled Particles after resampling.
 * @param weights_resampled Weights after resampling.
 * @param N_r Number of particles to resample.
 */
void ParticleFilter::SystematicResampling(const Eigen::MatrixXd &particles_ori,
                                          const Eigen::VectorXd &weights_ori_norm,
                                          Eigen::MatrixXd &particles_resampled,
                                          Eigen::VectorXd &weights_resampled,
                                          uint32_t N_r)
{
    uint32_t N = weights_ori_norm.size();

    Eigen::VectorXd weights_cum_sum = CalcWeightsCumSum(weights_ori_norm);

    uint32_t i = 0;

    // produces random values u0, uniformly distributed on the interval [0.0, 1.0 / N_r)
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_real_distribution<> uniform_dist(0.0, 1 / N_r);
    double u0 = uniform_dist(gen);

    for (size_t j = N - N_r; j < N; ++j)
    {
        // calculate u = u0 + (j - (N - N_r)) / N_r
        double u = u0 + (j - (N - N_r)) / N_r;

        // select the resampled particle
        while (weights_cum_sum(i) < u)
            ++i;

        particles_resampled(j) = particles_ori(i);
        weights_resampled(j) = 1 / N;
    }
}

残差重采样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * @brief Residual resampling method.
 *
 * @param particles_ori Particles before resampling.
 * @param weights_ori_norm Normalized weights before resampling.
 * @param particles_resampled Particles after resampling.
 * @param weights_resampled Weights after resampling.
 */
void ParticleFilter::ResidualResampling(const Eigen::MatrixXd &particles_ori,
                                        const Eigen::VectorXd &weights_ori_norm,
                                        Eigen::MatrixXd &particles_resampled,
                                        Eigen::VectorXd &weights_resampled)
{
    uint32_t N = weights_ori_norm.size();
    uint32_t j = 0;
    Eigen::VectorXi N_k1(N);

    // step1: deterministic copy sampling
    for (size_t i = 0; i < N; ++i)
    {
        N_k1(i) = std::floor(N * weights_ori_norm(i));

        for (size_t m = 0; m < N_k1(i); ++m)
        {
            particles_resampled(j) = particles_ori(i);
            weights_resampled(j) = 1 / N;
            ++j;
        }
    }

    // step2: residual random sampling
    uint32_t N_k2 = N - j;
    Eigen::VectorXd weights_residual_norm = (N * weights_ori_norm - N_k1) / N_k2;
    MultinomialResampling(particles_ori, weights_residual_norm, particles_resampled,
                          weights_resampled, N_k2);
}

5.2.6 状态估计

完成重采样后，我们将所有的重采样粒子及其对应的重采样权重（$\frac{1}{N}$）进行加权求和，便可得到系统最终的状态估计结果，即每个时刻无人车的位置、航向估计。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @brief Estimate the final state of system by combing all particles.
 *
 * @param particles_resampled Particles after resampling.
 * @param weights_resampled Weights after resampling.
 * @param particles_ori Particles before resampling.
 * @param weights_ori_norm Normalized weights before resampling.
 * @param weights_ori Non-normalized weights before resampling.
 * @return Eigen::Vector3d The final estimated state of system.
 */
inline Eigen::Vector3d EstimateState(const Eigen::MatrixXd &particles_resampled,
                                     const Eigen::VectorXd &weights_resampled,
                                     Eigen::MatrixXd &particles_ori,
                                     Eigen::VectorXd &weights_ori_norm,
                                     Eigen::VectorXd &weights_ori)
{
    particles_ori = particles_resampled;
    weights_ori = weights_resampled;
    weights_ori_norm = weights_resampled;

    return particles_ori * weights_ori_norm;
}

下面是我们的 main.cpp 中的内容。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include "ParticleFilter.h"

int main()
{
    ParticleFilter pf;                   // particle filter instance
    double x, y, theta;                  // gps measurement data
    double v, yaw_rate;                  // input control data
    std::vector<LandMark_Ego> lmrks_obs; // observed landmarks in local ego vehicle coordinate
    std::vector<LandMark_Map> lmrks_map; // map landmarks

    while (true)
    {
        pf.RecvRawData(x, y, theta, v, yaw_rate, lmrks_obs, lmrks_map);

        pf.Init(x, y, theta, pf.sigma_gps);
        pf.Predict(v, yaw_rate, pf.dt, pf.sigma_gps);
        pf.Update(lmrks_obs, pf.sensor_range, lmrks_map, pf.sigma_landmark);
        pf.NormalizeWeights(pf.weights_nonnormalized, pf.weights_normalized);
        pf.SystematicResampling(pf.particles, pf.weights_normalized,
                                pf.particles_re, pf.weights_re, pf.n_p);
        pf.estimated_state = pf.EstimateState(pf.particles_re, pf.weights_re,
                                              pf.particles, pf.weights_normalized,
                                              pf.weights_nonnormalized);
    }

    return 0;
}

点击这里下载完整代码工程。

6 总结

首先，我们回顾了用于解决线性高斯问题的卡尔曼滤波，用于解决非线性高斯问题的扩展卡尔曼滤波与无迹卡尔曼滤波，为解决强非线性非高斯问题我们引入了粒子滤波的概念。

粒子滤波基于随机采样实现。我们从蒙特卡罗方法讲起，为解决原分布难以采样甚至无法采样的问题引入了重要性采样。为序贯地进行粒子采样，并递推地更新粒子的重要性权重，又引入了序贯重要性采样。序贯重要性采样存在粒子退化问题，为应对该问题，可以选择恰当的建议分布并实施重采样步骤，文中介绍了四种重采样方法。通过将系统的状态转移概率分布选择为建议分布，并辅以重采样方法，我们由序贯重要性采样得到了采样重要性重采样滤波器。

最后，我们优化重构了 Udacity 工程框架，完整展示了如何通过粒子滤波实现无人车的匹配定位。

参考

  1. Kalman-and-Bayesian-Filters-in-Python
  2. b 站徐亦达机器学习：Particle Filter 粒子滤波
  3. 概率机器人——粒子滤波
  4. 维基百科：Particle filter
  5. 维基百科：大数定律
  6. 粒子滤波理论、方法及其在多目标跟踪中的应用
  7. MathWorks：Particle Filter Parameters
  8. 粒子滤波（PF：Particle Filter）
  9. b 站贝叶斯滤波与卡尔曼滤波第九讲：粒子滤波原理详述
  10. b 站贝叶斯滤波与卡尔曼滤波第十讲：重采样
  11. b 站贝叶斯滤波与卡尔曼滤波第十二讲：粒子滤波拾遗——采样方法、预测方程
  12. 粒子滤波器
  13. 粒子滤波
  14. A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking
  15. Particle Filter Tutorial 粒子滤波：从推导到应用（一）
  16. Particle Filter Tutorial 粒子滤波：从推导到应用（二）
  17. Particle Filter Tutorial 粒子滤波：从推导到应用（三）
  18. Particle Filter Tutorial 粒子滤波：从推导到应用（四）
  19. 百度文库：粒子滤波理论
  20. 粒子滤波原理
  21. 《卡尔曼滤波与组合导航原理》（第 3 版）
  22. 《概率机器人》
  23. Bayesian Signal Processing : Classical, Modern, and Particle Filtering Methods
  24. Computer Vision - Principles, Algorithms, Applications, Learning (5th)
  25. Novel approach to nonlinear/non-Gaussian Bayesian state estimation
  26. Monte Carlo Filter and Smoother for Non-Gaussian Nonlinear State Space Models
  27. On Resampling Algorithms For Particle Filters
  28. Resampling Methods for Particle Filtering-Classification, implementation, and strategies
  29. MathWorks: Particle filter tutorial
  30. udacity/CarND-Kidnapped-Vehicle-Project
  31. 粒子滤波简介
  32. 无人驾驶技术入门（二十）| 手把手教你用粒子滤波实现无人车定位
  33. std::uniform_real_distribution
  34. （十二）无人驾驶中的坐标转换
猜你喜欢
Thank you for your donate!