从贝叶斯滤波到卡尔曼滤波

目录

0 前言

卡尔曼滤波（Kalman Filter，KF）以贝叶斯滤波为理论基础，并通过假设状态量随机变量（以下简称状态量）、观测量均服从正态分布，假设过程噪声、观测噪声均服从均值为 0 的正态分布，以及假设状态转移函数和观测函数均为线性函数，实现对连续型随机过程的递推状态估计。简言之，卡尔曼滤波是在贝叶斯滤波框架下求解线性高斯问题。

1 贝叶斯滤波的三大概率密度函数

在此前的文章《从概率到贝叶斯滤波》中，已经讲到贝叶斯滤波的先验概率密度函数、似然概率密度函数和后验概率密度函数：

(1) 先验概率密度函数

$$f_{X_k}^-(x)=\int_{-\infty}^{+\infty}f_{Q_k}[x-f(v)]f_{X_{k-1}}^+(v)\mathrm{d}v$$

(2) 似然概率密度函数

$$f_{Y_k|X_k}(y_k \ | \ x) = f_{R_k}[y_k-h(x)]$$

(3) 后验概率密度函数

$$f_{X_k}^+(x)=\eta_k·f_{R_k}[y_k-h(x)]·f_{X_k}^-(x)$$

其中，后验概率密度函数中的归一化常数 $\eta_k$ 为：

$$\eta_k=\left\{\int_{-\infty}^{+\infty}f_{R_k}[y_k-h(x)]f_{X_k}^-(x)\mathrm{d}x\right\}^{-1}$$

2 卡尔曼滤波的假设

卡尔曼滤波以贝叶斯滤波为理论基础，并作了六个前提假设：

(1) 假设一：状态量服从正态分布

$$X \sim \mathcal{N}(\mu_X, \ \sigma_X^2)$$

(2) 假设二：观测量服从正态分布

$$Y \sim \mathcal{N}(\mu_Y, \ \sigma_Y^2)$$

(3) 假设三：过程噪声服从均值为 0 的正态分布

$$Q \sim \mathcal{N}(0, \ \sigma_Q^2)$$

(4) 假设四：观测噪声服从均值为 0 的正态分布

$$Q \sim \mathcal{N}(0, \ \sigma_R^2)$$

(5) 假设五：状态转移函数为线性函数

$$f(X_k)=F*X_{k-1}+B*u_k$$

其中，$F$ 为状态转移比例项，对于单一状态量的卡尔曼滤波中，$F$ 为一常数；$B$ 为控制比例项，$u_k$ 为控制量，$B$ 和 $u_k$ 的乘积可视为线性状态转移函数中的截距项。在简单的系统中，常常没有控制项 $B$ 和 $u_k$。

(6) 假设六：观测函数为线性函数

$$h(X_k)=H*X_k$$

$H$ 为观测比例项，对于单一状态量的卡尔曼滤波中，$H$ 为一常数。

3 卡尔曼滤波的公式推导

3.1 预测步的两个公式

根据假设一，$k-1$ 时刻状态量 $X_{k-1}$ 服从均值为 $\mu_{k-1}^+$，方差为 ${\sigma_{k-1}^+}^2$ 的正态分布：

$$X_{k-1} \sim \mathcal{N}(\mu_{k-1}^+, \ {\sigma_{k-1}^+}^2)$$

$X_{k-1}$ 的后验概率密度函数为：

$$f_{X_{k-1}}^+=\frac{1}{\sigma_{k-1}^+\sqrt{2\pi}}e^{-\frac{(x-\mu_{k-1}^+)^2}{2{\sigma_{k-1}^+}^2}}$$

结合假设三与假设五，k 时刻状态量 $X_k$ 的先验概率密度函数为：

$$\begin{aligned} f_{X_k}^-(x) & = \int_{-\infty}^{+\infty}f_{Q_k}[x-f(v)]f_{X_{k-1}}^+(v)\mathrm{d}v \\ & = \int_{-\infty}^{+\infty}\frac{1}{\sigma_{Q_k}\sqrt{2\pi}}e^{-\frac{(x-F*v-B*u_k)^2}{2{\sigma_{Q_k}}^2}}*\frac{1}{\sigma_{k-1}^+\sqrt{2\pi}}e^{-\frac{(v-\mu_{k-1}^+)^2}{2{\sigma_{k-1}^+}^2}}\mathrm{d}v \end{aligned}$$

对于 $f_{X_k}^-(x)$ 的推导，有三种方法：

• Mathematica 软件做符号推导
• 复变函数留数定理
• 傅里叶变换 + 卷积

这里使用 Mathematica 软件做符号推导，创建 WolframScript（.wls）脚本文件，创建 $f_{X_k}^-(x)$ 公式：

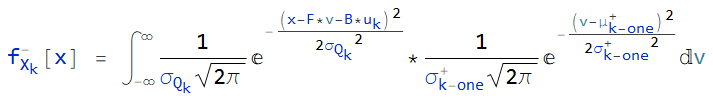
其中，${\sigma_{Q_k}}^2$ 表示 k 时刻过程噪声的方差；$\mu_{k-one}^+$ 表示 $k-1$ 时刻状态量的后验概率密度函数均值；${\sigma_{k-one}^+}^2$ 表示 $k-1$ 时刻状态量的后验概率密度函数方差。

运行代码进行化简，得到如下条件表达式结果：

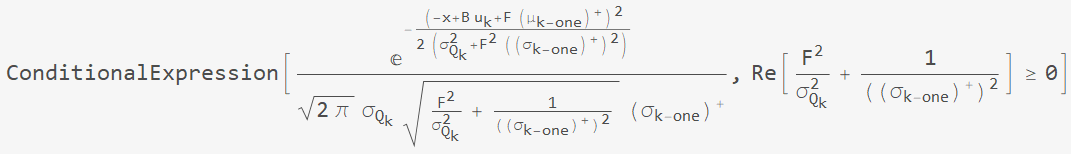
条件表达式中的条件显然成立，整理表达式形式可知，先验概率密度函数 $f_{X_k}^-(x)$ 为正态分布函数，均值和方差分别为：

$$\mu_k^- = F*\mu_{k-1}^++B*u_k \tag{3.1}$$ $${\sigma_k^-}^2 = F^2*{\sigma_{k-1}^+}^2+{\sigma_{Q_k}}^2 \tag{3.2}$$

3.2 更新步的三个公式

结合假设四、假设六、公式 (3.1)、公式 (3.2)，可知，k 时刻状态量 $X_k$ 的后验概率密度函数为：

$$\begin{aligned} f_{X_k}^+(x) & = \eta_k·f_{R_k}[y_k-h(x)]·f_{X_k}^-(x) \\ & = \eta_k*\frac{1}{\sigma_{R_k}\sqrt{2\pi}}e^{-\frac{(y_k-H*x)^2}{2{\sigma_{R_k}}^2}}*\frac{1}{\sigma_{k}^-\sqrt{2\pi}}e^{-\frac{(x-\mu_{k}^-)^2}{2{\sigma_{k}^-}^2}} \end{aligned}$$

其中，归一化常数 $\eta_k$ 为：

$$\eta_k=\int_{-\infty}^{\infty}\frac{1}{\sigma_{R_k}\sqrt{2\pi}}e^{-\frac{(y_k-H*x)^2}{2{\sigma_{R_k}}^2}}*\frac{1}{\sigma_{k}^-\sqrt{2\pi}}e^{-\frac{(x-\mu_{k}^-)^2}{2{\sigma_{k}^-}^2}}\mathrm{d}x$$

创建 WolframScript（.wls）脚本文件，创建 $f_{X_k}^+(x)$ 公式：

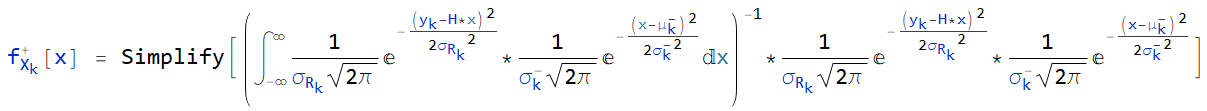
其中，${\sigma_{R_k}}^2$ 表示 k 时刻观测噪声的方差；$y_k$ 表示 k 时刻观测量的取值。Simplify[] 函数的使用是为了简化结果。

运行代码进行化简，得到如下条件表达式结果：

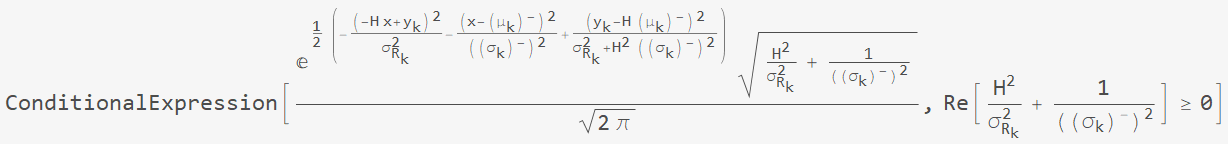
条件表达式中的条件显然成立，整理表达式形式可知后验概率密度函数 $f_{X_k}^+(x)$ 的均值和方差分别为：

$$\mu_k^+ = \mu_k^-+K*(y_k-H*\mu_k^-) \tag{3.3}$$ $${\sigma_k^+}^2 = (1-K*H)*{\sigma_k^-}^2 \tag{3.4}$$

$\mu_k^+$ 即 k 时刻状态量 $X_k$ 的后验估计 $\hat{x}_k^+$。其中，$K$ 被称为卡尔曼增益系数：

$$K=\frac{H*{\sigma_k^-}^2}{H^2*{\sigma_k^-}^2+{\sigma_{R_k}}^2} \tag{3.5}$$

卡尔曼增益系数 $K$ 可变形为：

$$K=\frac{H*{\sigma_k^-}^2}{H^2*{\sigma_k^-}^2+{\sigma_{R_k}}^2} = \frac{H}{H^2+{\sigma_{R_k}}^2/{\sigma_k^-}^2}$$

当 ${\sigma_{R_k}}^2 \gg {\sigma_k^-}^2$ 时，$K\to0$，故

$$\mu_k^+ = \mu_k^-+K*(y_k-H*\mu_k^-) \to \mu_k^-$$

此时，后验估计结果倾向于预测；

当 ${\sigma_{R_k}}^2 \ll {\sigma_k^-}^2$ 时，$K\to\frac{1}{H}$，故

$$\mu_k^+ = \mu_k^-+K*(y_k-H*\mu_k^-) \to \frac{y_k}{H}$$

此时，后验估计结果倾向于观测。

点击这里下载我的 WolframScript（.wls）脚本文件。

4 矩阵形式的卡尔曼滤波

上文内容所描述的是一维的卡尔曼滤波，当状态量和观测量不再是单一的随机变量而是由多个随机变量组成的序列时，卡尔曼滤波中各个量的维数也将随之改变：

• 状态量 $X$ 由随机变量演变为随机向量，随机向量中的每一个分量为一个状态量随机变量。维数为 $n_X \times 1$
• 状态转移比例项 $F$ 演变为矩阵，维数为 $n_X \times n_X$
• 控制量 $u_k$ 演变为矩阵，维数为 $n_u \times 1$
• 控制比例项 $B$ 演变为矩阵，维数为 $n_X \times n_u$
• 状态量概率密度函数均值 $\mu$ 演变为矩阵，维数为 $n_X \times 1$
• 状态量概率密度函数方差 $\sigma^2$ 演变为协方差矩阵，用 $\Sigma$ 表示，维数为 $n_X \times n_X$
• 过程噪声方差 ${\sigma_Q}^2$ 演变为协方差矩阵，用 $\Sigma_Q$ 表示，维数为 $n_X \times n_X$
• 观测量 $Y$ 由随机变量演变为随机向量，随机向量中的每一个分量为一个观测量随机变量。维数为 $n_Y \times 1$
• 观测值 $y_k$ 由单一值演变为由单一值组成的值矩阵，维数为 $n_Y \times 1$
• 观测比例项 $H$ 演变为矩阵，维数为 $n_Y \times n_X$
• 观测噪声方差 ${\sigma_R}^2$ 演变为协方差矩阵，用 $\Sigma_R$ 表示，维数为 $n_Y \times n_Y$
• 卡尔曼增益系数 $K$ 演变为矩阵，维数为 $n_X \times n_Y$

对应的五个公式演变为：

$$\mu_k^- = F*\mu_{k-1}^++B*u_k \tag{4.1}$$ $$\Sigma_k^- = F*\Sigma_{k-1}^+*F^T+{\Sigma_{Q_k}} \tag{4.2}$$ $$\mu_k^+ = \mu_k^-+K*(y_k-H*\mu_k^-) \tag{4.3}$$ $$\Sigma_k^+ = (I-K*H)*\Sigma_k^- \tag{4.4}$$ $$K=\Sigma_k^-*H^T*(H*\Sigma_k^-*H^T+{\Sigma_{R_k}})^{-1} \tag{4.5}$$

公式 (4.3) 中 $\mu_k^+$ 即 k 时刻状态量 $X_k$ 的后验估计 $\hat{x}_k^+$，$y_k-H*\mu_k^-$ 常被称为残差（Residual）或新息（Innovation）；公式 (4.4) 中的 $I$ 代表单位矩阵，维数为 $n_X \times n_X$。

从结果中还可以发现，外部控制项 $B*u_k$ 通过影响先验估计均值间接影响了后验估计均值，但对后验估计方差没有影响。

5 应用实例

卡尔曼滤波的应用实例可参考此前的学习文章《（十三）手把手教你写卡尔曼滤波器》，文章中的应用场景是使用激光雷达（Lidar）对匀速直线运动（Constant Velocity，CV）目标的测距过程。

博主工作中使用卡尔曼滤波对路口前的停止线（来自单目前向视觉）纵向距离进行了估计，系统模型抽象为匀加速直线运动（Constant Acceleration，CA），此时的状态转移函数 $f(x)$ 中存在外部控制项 $B*u_k$，停止线纵向距离估计结果用于下游规划控制模块的纵向速度规划输入参考。

参考

1. b 站忠实的王大头《贝叶斯滤波与卡尔曼滤波》第七讲：卡尔曼滤波
2. 无人驾驶技术入门（十三）| 手把手教你写卡尔曼滤波器
3. How a Kalman filter works, in pictures
4. 详解卡尔曼滤波原理
5. Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation

---