本文章学习总结自知乎大 V陈光的《无人驾驶干货铺》专栏，查阅原文请移步这里

1 正文

简单来讲，卡尔曼滤波器就是根据上一时刻的状态，预测当前时刻的状态，将预测的状态量与当前时刻的观测量进行加权，加权后的结果才认为是当前实际的状态量，而非仅听信当前的观测量。卡尔曼滤波过程可主要概括为以下三步：

(1) 初始化（Initialization）

假设有个小车在道路上向右侧做匀速运动，在左侧安装了一个可以测量小车距离和速度的传感器，传感器每 1 秒测一次小车的位置 $s$ 和速度 $v$，如下图所示：

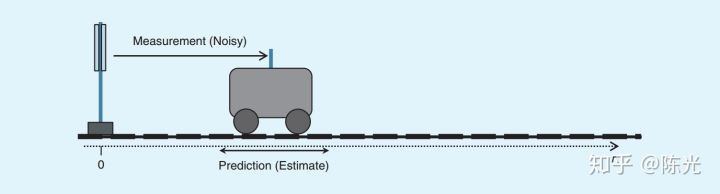
用向量 $x_t$ 来表示当前小车的状态，该向量也是最终的输出结果，被称作状态向量（state vector）：

$x_t= \begin{bmatrix} s_t \\ v_t \end{bmatrix}$

由于测量误差的存在，传感器无法直接获取小车位置的真值，只能获取在真值附近的一个近似值，可以假设测量值在真值附近服从高斯分布。如下图所示，测量值分布在红色区域内的左侧或右侧，真值则在红色区域的波峰处：

由于是第一次测量，没有小车的历史信息，认为小车在 $t=1$ 秒时的状态量 $x_1$ 与观测量 $z_1$ 相等：

$x_1=z_1= \begin{bmatrix} s_1 \\ v_1 \end{bmatrix}$

(2) 预测（Prediction）

预测是卡尔曼滤波中很重要的一步，这一步相当于使用历史信息对未来的位置进行推测。根据第 1 秒小车的位置和速度，可以推测第 2 秒时，小车所在的位置应该如下图所示：

会发现，图中红色区域的范围变大了，这是因为预测时加入了速度估计的噪声，是一个放大不确定性的过程。根据小车第 1 秒的状态量进行预测，得到预测的第 2 秒的状态量 $x_{pre}$：

$x_{pre}= \begin{bmatrix} s_1+v_1 \\ v_1 \end{bmatrix}$

其中，下脚标 $pre$ 是 prediction 的简称。时间间隔为 1 秒，所以预测位置为距离+速度*1，由于小车做匀速运动，因此速度保持不变。

(3) 观测（Measurement）

在第 2 秒时，传感器对小车的位置做了一次观测，认为小车在第 2 秒时的观测量为 $z_2$：

$z_2= \begin{bmatrix} s_2 \\ v_2 \end{bmatrix}$

显然，第二次观测的结果也是存在误差的，将预测的小车位置与实际观测到的小车位置放在同一个图上，即可看到：

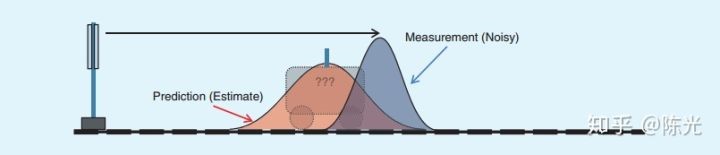
图中红色区域为预测的小车位置，蓝色区域为第 2 秒的观测结果。显然，这两个结果都在真值附近。为得到尽可能接近真值的结果，将这两个区域的结果进行加权，取加权后的值作为第 2 秒的状态量。为了方便理解，可以将第 2 秒的状态量写成：

$x_2=w_1*x_{pre}+w_2*z_2$

其中，$w_1$ 为预测结果的权值，$w_2$ 为观测结果的权值。两个权值的计算是根据预测结果和观测结果的不确定性来的，这个不确定性就是高斯分布中方差的大小，方差越大，波形分布越广，不确定性越高，给的权值越低。加权后的状态向量的分布可以用下图中绿色区域表示：

可以发现，绿色区域的方差均小于红色区域和蓝色区域，原因是进行加权运算时，需要将两个高斯分布进行乘法运算，得到的新的高斯分布的方差比两个做乘法的高斯分布都小。两个不那么确定的分布，最终得到了一个相对确定的分布。

第 1 秒的初始化以及第 2 秒的预测、观测，实现了卡尔曼滤波的第一个周期。同样地，根据第 2 秒的状态量做第 3 秒的预测，再与第 3 秒的观测量进行加权，就得到了第 3 秒的状态量；再根据第 3 秒的状态量做第 4 秒的预测，再与第 4 秒的观测量进行加权，就得到了第 4 秒的状态量。以此往复，就实现了一个真正意义上的卡尔曼滤波器。卡尔曼滤波器的理论公式如下所示：

下面结合上面的公式，用 C++代码实现初始化、预测、观测的过程。由于公式中涉及大量的矩阵转置和求逆运算，使用开源的矩阵运算库——Eigen。

代码：初始化（Initialization）

初始化阶段，需要将各个变量初始化，对于不同的运动模型，其状态向量不同，对于上文中小车的例子，只需距离 $s$ 和速度 $v$ 就可以表示小车的状态；再比如一个二维空间中的点，需要 $x$ 方向上的距离和速度及 $y$ 方向上的距离和速度才能表示其状态，这样的状态量就有 4 个变量。因此使用 Eigen 库中非定长的数据结构，下图中的VerctorXd表示 X 维的列向量，其中的元素数据类型为double：

#ifndef KALMAN_FILTER_
#define KALMAN_FILTER_
#include "Eigen/Dense"

class KalmanFilter
{
public:
    KalmanFilter()
    {
        is_initialized = false;
    }

    ~KalmanFilter();

    void Initialization(Eigen::VectorXd x_in)
    {
        x_ = x_in;
    }

private:
    bool is_initialized; //flag of initialization
    Eigen::VectorXd x_;   //state vector
};

#endif

这里，新建了一个KalmanFilter类，其中定义了一个叫做x_的变量，表示小车的状态向量。

代码：预测（Prediction）

完成初始化后，开始写 Prediction 部分的代码。首先是公式：

$x^\prime=Fx+u$

这里的 $x$ 为上一时刻状态量，通过左乘一个状态转移矩阵（state transistion matrix）$F$，再加上外部影响 $u$，得到预测的当前时刻的状态量 $x^\prime$。以 2 维的匀速运动为例，$x$ 为：

$x= \begin{bmatrix} s_x \\ s_y \\ v_x \\ v_y \end{bmatrix}$

对于匀速运动模型，经过时间 $\Delta t$ 后的预测状态量为：

$x^\prime= \begin{bmatrix} s_x +v_x\Delta t \\ s_y +v_y\Delta t \\ v_x \\ v_y \end{bmatrix}$

由于假设当前运动为匀速运动，加速度为 0，加速度不会对预测造成影响，即：

$u=0$

公式 $x^\prime=Fx+u$ 演变为：

$\begin{bmatrix} s_x +v_x\Delta t \\ s_y +v_y\Delta t \\ v_x \\ v_y \end{bmatrix}= \begin{bmatrix} 1 & 0 & \Delta t & 0 \\ 0 & 1 & 0 & \Delta t \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} s_x \\ s_y \\ v_x \\ v_y \end{bmatrix}+ \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}$

如果换成匀加速运动模型，就可以引入加速度 $a_x$ 和 $a_y$，$u$ 变为：

$u= \begin{bmatrix} \frac{1}{2}a_x\Delta t^2 \\ \frac{1}{2}a_y\Delta t^2 \\ a_x\Delta t \\ a_y\Delta t \end{bmatrix}$

由于每次预测时，$\Delta t$ 的大小不固定，因此专门写一个函数SetF()：

void SetF(Eigen::MatrixXd F_in)
{
    F_ = F_in;
}

再看预测模块的第二个公式：

$P^\prime=FPF^T+Q$

该公式中，$P$ 被称为状态协方差矩阵（state covariance matrix），表示系统的不确定程度，$P$ 在卡尔曼滤波器初始化时会很大，随着越来越多的数据注入滤波器中，不确定程度会逐渐减小；$Q$ 是过程噪声协方差矩阵（process noise covariance matrix），即无法用 $x^\prime=Fx+u$ 表示的噪声，比如车辆运动时突然到了上坡，这个影响是无法用之前的状态转移估计的。以激光雷达为例，激光雷达只能测量点的位置，无法测量点的速度，因此对于激光雷达的协方差矩阵来说，对于位置信息，其测量较准确，不确定度较低；对于速度信息，不确定度较高。因此可以认为此处的 $P$ 为：

$P= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 100 & 0 \\ 0 & 0 & 0 & 100 \end{bmatrix}$

由于 $Q$ 对整个系统存在影响，但又不能确定对系统的影响有多大。工程上，一般将 $Q$ 设置为单位矩阵参与运算，即：

$Q= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

根据以上内容和公式：

$\begin{cases} x^\prime=Fx+u \\ P^\prime=FPF^T+Q \end{cases}$

就可以写出预测模块的代码了：

void Prediction()
{
    x_ = F_ * x_;
    Eigen::MatrixXd Ft = F_.transpose();
    P_ = F_ * P_ * Ft + Q_;
}

代码：观测（Measurement）

观测模块的第一个公式是：

$y=z-Hx^\prime$

这个公式计算的是实际观测量 $z$ 与状态量预测值 $x^\prime$ 之间的差值 $y$。不同传感器的观测量一般不同，比如激光雷达测量的位置信号为 $x$ 方向和 $y$ 方向上的距离，毫米波雷达测量的是位置和角度信息。因此需要将状态量左乘一个矩阵 $H$，才能与观测量进行相应的运算，$H$ 被称为测量矩阵（Measurement Matrix）。激光雷达的观测量为：

$z= \begin{bmatrix} x_m \\ y_m \end{bmatrix}$

其中 $x_m$ 和 $y_m$ 分别表示 $x$ 方向和 $y$ 方向上的测量值。由于 $x^\prime$ 是一个 4*1 的列向量，如果要与一个 2*1 的列向量 $z$ 进行减运算，需要左乘一个 2*4 的矩阵：

$\begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix}= \begin{bmatrix} x_m \\ y_m \end{bmatrix}- \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} s_x +v_x\Delta t \\ s_y +v_y\Delta t \\ v_x \\ v_y \end{bmatrix}$

意即，对于激光雷达而言，测量矩阵 $H$ 为：

$H= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{bmatrix}$

求得 $y$ 后，对 $y$ 乘以一个加权量，再加到原来的状态量预测量上去，就可以得到一个既考虑了观测量，又考虑了预测模型位置的状态量了。对于权值 $K$ 的计算，看下面的两个公式：

$\begin{cases} S=HP^\prime H^T+R \\ K=P^\prime H^TS^{-1} \end{cases}$

权值 $K$ 被称为卡尔曼增益（Kalman Gain），$R$ 是测量噪声协方差矩阵（measurement noise covariance matrix），表示的是测量值与真值之间的差值。一般情况下，传感器厂家会提供该值。$S$ 只是为了简化公式，写的一个临时变量。最后两个公式：

$\begin{cases} x=x^\prime+Ky \\ P=(I-KH)P^\prime \end{cases}$

上述两个公式，实际上完成了卡尔曼滤波器的闭环，第一个公式是完成了当前状态量 $x$ 的更新，不仅考虑了上一时刻状态量的预测量，也考虑了观测量和整个系统的噪声；第二个公式根据卡尔曼增益，更新了系统的不确定度 $P$，用于下一个周期的运算，该公式中的 $I$ 为单位矩阵，维数为状态量的行数。将观测模块的五个公式写成代码如下：

#ifndef KALMAN_FILTER_
#define KALMAN_FILTER_
#include "Eigen/Dense"

class KalmanFilter
{
  public:
    KalmanFilter()
    {
        is_initialized = false;
    }

    ~KalmanFilter();

    // get state vector
    Eigen::VectorXd GetX()
    {
        return x_;
    }

    // get flag of initialization
    bool IsInitialized()
    {
        return is_initialized;
    }

    // initialize kalman filter
    void Initialization(Eigen::VectorXd x_in)
    {
        x_ = x_in;
        is_initialized = true;
    }

    void SetF(Eigen::MatrixXd F_in)
    {
        F_ = F_in;
    }

    void SetP(Eigen::MatrixXd P_in)
    {
        P_ = P_in;
    }

    void SetQ(Eigen::MatrixXd Q_in)
    {
        Q_ = Q_in;
    }

    void SetH(Eigen::MatrixXd H_in)
    {
        H_ = H_in;
    }

    void SetR(Eigen::MatrixXd R_in)
    {
        R_ = R_in;
    }

    // predict state vector and state covariance matrix
    void Prediction()
    {
        x_ = F_ * x_;
        Eigen::MatrixXd Ft = F_.transpose();
        P_ = F_ * P_ * Ft + Q_;
    }

    // update state vector and state covariance matrix
    void MeasurementUpdate(const Eigen:: VectorXd &z)
    {
        Eigen::VectorXd y = z - H_ * x_;
        Eigen::MatrixXd S = H_ * P_ * H_.transpose() + R_;
        // Kalman Gain
        Eigen::MatrixXd K = P_ * H_.transpose() * S.inverse();
        // estimate state vector
        x_ = x_ + K * y;
        int size = x_.size;
        Eigen::Matrix2Xd I = Eigen::MatrixXd::Identity(size, size);
        // update state covariance matrix
        P_ = (I - K * H_) * P_;
    }

  private:
    bool is_initialized; // flag of initialization
    Eigen::VectorXd x_;  // state vector
    Eigen::MatrixXd F_;  // state transition matrix
    Eigen::MatrixXd P_;  // state covariance matrix
    Eigen::MatrixXd Q_;  // process noise covariance matrix
    Eigen::MatrixXd H_;  // measurement matrix
    Eigen::MatrixXd R_;  // measurement noise covariance matrix
};

#endif

可以发现MeasurementUpdate()函数的形参为“常引用”类型，这样既兼顾了参数传递效率（因为是引用，所以无需为传入的参数申请物理内存用以保存其值），又保证了数据安全（因为参数被const修饰了）。以激光雷达数据为例，使用以上滤波器，代码如下：

#include "KalmanFilter.h"
#include <iostream>

int main()
{
    double Sx = 0.0, Sy = 0.0;
    double last_timestamp = 0.0, now_timestamp = 0.0;
    KalmanFilter kf;
    while (GetLidarData(Sx, Sy, now_timestamp))
    {
        // initialize kalman filter
        if (!kf.IsInitialized())
        {
            last_timestamp = now_timestamp;
            Eigen::VectorXd x_in(4, 1);
            x_in << Sx, Sy, 0.0, 0.0;
            kf.Initialization(x_in);
            // set state covariance matrix
            Eigen::MatrixXd P_in(4, 4);
            P_in << 1.0, 0.0, 0.0, 0.0,
                    0.0, 1.0, 0.0, 0.0,
                    0.0, 0.0, 100.0, 0.0,
                    0.0, 0.0, 0.0, 100.0;
            kf.SetP(P_in);
            // set process noise covariance matrix
            Eigen::MatrixXd Q_in(4, 4);
            Q_in << 1.0, 0.0, 0.0, 0.0,
                    0.0, 1.0, 0.0, 0.0,
                    0.0, 0.0, 1, 0.0,
                    0.0, 0.0, 0.0, 1;
            kf.SetQ(Q_in);
            // set measurement matrix
            Eigen::MatrixXd H_in(2, 4);
            H_in << 1.0, 0.0, 0.0, 0.0,
                    0.0, 1.0, 0.0, 0.0;
            kf.SetH(H_in);
            // set measurement noise covariance matrix
            // R is provided by sensor supplier, in datasheet
            Eigen::MatrixXd R_in(2, 2);
            R_in << 0.0225, 0.0,
                    0.0, 0.0225;
            kf.SetR(R_in);
            continue;
        }
        // set state transition matrix
        double dt = now_timestamp - last_timestamp;
        Eigen::MatrixXd F_in(4, 4);
        F_in << 1.0, 0.0, dt, 0.0,
                0.0, 1.0, dt, 0.0,
                0.0, 0.0, 1, 0.0,
                0.0, 0.0, 0.0, 1;
        kf.SetF(F_in);
        // predict state vector x and state covariance matrix P
        kf.Prediction();
        // update state vector x and state covariance matrix P
        Eigen::VectorXd z(2, 1);
        z << Sx, Sy;
        kf.MeasurementUpdate(z);
        Eigen::VectorXd x_out(4, 1);
        // output result
        x_out = kf.GetX();
        std::cout << "Kalman filter output Sx is: " << x_out(0)
                   << ", output Sy is: " << x_out(1) << std::endl;
        return 0;
    }
}

其中，GetLidarData()函数除了获取点的位置信息 $S_x$ 和 $S_y$ 外，还获取了当前时刻的时间戳，用于计算前后两帧的时间差 $\mathrm{d}t$。在经典卡尔曼滤波器基础上，还有扩展卡尔曼滤波器（EKF）和无迹卡尔曼滤波器（UKF），它们与经典卡尔曼滤波器的最大区别是状态转移矩阵 $F$ 和测量矩阵 $H$ 的不同。下图（原图出自这里）很形象地说明了经典卡尔曼滤波器的原理：

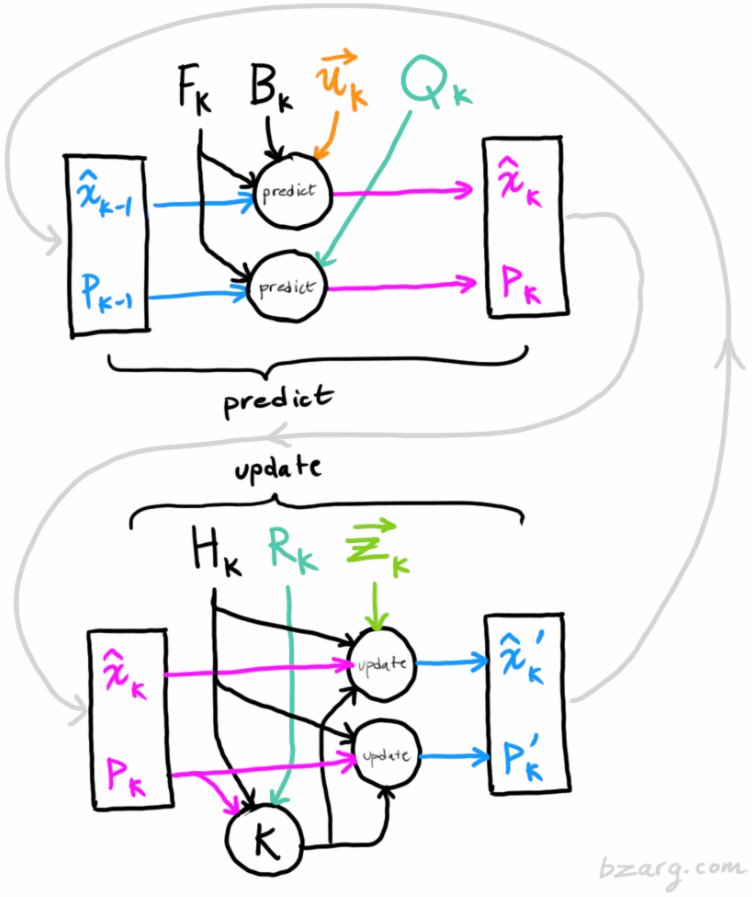
2 参考

无人驾驶技术入门（十三）| 手把手教你写卡尔曼滤波器
How a Kalman filter works, in pictures

输出倒逼思考

（十三）手把手教你写卡尔曼滤波器

1 正文

2 参考