输出倒逼思考

0%

最小二乘法多项式曲线拟合数学原理及其 C++ 实现

发表于
分类于 ， Valine：
自动驾驶开发中经常涉及到多项式曲线拟合，本文详细描述了使用最小二乘法进行多项式曲线拟合的数学原理，通过样本集构造范德蒙德矩阵，将一元 N 次多项式非线性回归问题转化为 N 元一次线性回归问题，并基于线性代数 C++ 模板库——Eigen 进行了实现，最后，比较了几种实现方法在求解速度与求解精度上的差异。

目录

目录-最小二乘法多项式曲线拟合数学原理及其 C++ 实现

0 前言

自动驾驶开发中经常涉及到多项式曲线拟合，本文详细描述了使用最小二乘法进行多项式曲线拟合的数学原理，通过样本集构造范德蒙德矩阵，将一元 N 次多项式非线性回归问题转化为 N 元一次线性回归问题，并基于线性代数 C++ 模板库——Eigen 进行了实现，最后，比较了几种实现方法在求解速度与求解精度上的差异。

1 符号约定

本文中对所使用的数学符号做如下约定：

  • 简体小写字母：标量。例如，$s$、$\theta_0$。注意，本文中的微分符号 $d$ 也使用简体小写字母
  • 粗体小写字母：向量。例如，$\boldsymbol{\theta}$、$\mathbf{y}$、$\mathbf{y_r}$
  • 粗体大写字母：矩阵。例如，$\mathbf{X}$、$\mathbf{X_v}$

2 最小二乘法概述

最小二乘法（Least Square Method，LSM）通过最小化误差（也叫残差）的平方和寻找数据的最优函数匹配。

假设给定一组样本数据集 $P(x, y)$，$P$ 内各数据点 $P_i(x_i, y_i) (i=1, 2, 3, …, m)$ 来自于对多项式

的多次采样，其中：

  • $m$ 为样本维度
  • $n$ 为多项式阶数
  • $\theta_j (j=0,1, 2, …, n)$ 为多项式的各项系数

样本数据集 $P$ 内各数据点的误差平方和 $s$ 为：

最小二乘法认为，最优函数的各项系数 $\theta_j$ 应使得误差平方和 $s$ 取得极小值。最小二乘法与极大似然估计有着密切的联系，关于最小二乘法的数学本质可参考文章《如何理解最小二乘法？》。

3 数学推导

3.1 代数法

由于最优函数的各项系数 $\theta_j$ 使得误差平方和 $s$ 取得极小值，因而，对于最优函数而言，其误差平方和 $s$ 对各多项式系数 $\theta_j$ 的偏导数应满足：

注意，式 (3.1) 最后的 0 为标量，应与下文中的零向量 $\mathbf{0}$ 进行区分。式 (3.1) 的推导用到了两个知识点：

  • ① → ②：多个函数的和的偏导数等于各个函数的偏导数的和
  • ② → ③：复合函数求偏导，将 $\theta_0+\theta_1x_i+\theta_2x_i^2+···+\theta_jx_i^j+···+\theta_nx_i^n-y_i$ 视作一个整体，运用链式法则求解

由式 (3.1) 我们可以进一步得到：

将 $j=0,1, 2, …, n$ 分别代入式 (3.2)，有：

我们将式 (3.3) 转化为矩阵形式，令：

则有：

使用样本数据集构造出矩阵 $\mathbf{X}$ 和向量 $\mathbf{y}$ 后，便可由式 (3.5) 解得最优函数的系数向量 $\boldsymbol{\theta}$。

3.2 矩阵法

在代数法中，构造矩阵 $\mathbf{X}$ 和向量 $\mathbf{y}$ 较为繁琐且计算量大，我们尝试直接将误差平方和 $s$ 拆解为矩阵形式。令：

则误差平方和 $s$ 可写成：

$\mathbf{X_v}$ 是一个范德蒙矩阵（Vandermonde Matrix），$\boldsymbol{\theta}$ 仍然是多项式系数构成的系数向量，$\mathbf{y_r}$ 是样本数据集的输出向量。对于最优函数，应满足：

注意，式 (3.8) 中的 $\mathbf{0}$ 为向量。$\frac{\partial{s}}{\partial{\boldsymbol{\theta}}}$ 是标量对向量的导数，这里我们不直接推导它，而是从推导 $s$ 的微分 $ds$ 开始：

式 (3.9) 的推导运用了几条基础运算法则：

  • ① → ②：$d(\mathbf{AB})=(d\mathbf{A})\mathbf{B}+\mathbf{A}(d\mathbf{B})$
  • ② → ③：$d\mathbf{A}^\mathrm{T}=(d\mathbf{A})^\mathrm{T}$
  • ③ → ④：$d(\mathbf{A\pm B})=d\mathbf{A}\pm d\mathbf{B}$，① → ② 中的法则，向量常量的微分为零向量 $\mathbf{0}$
  • ④ → ⑤：对于同维的列向量 $\mathbf{u}$ 和 $\mathbf{v}$，它们的内积满足 $\langle\mathbf{u},\mathbf{v}\rangle=\mathbf{u}^\mathrm{T}\mathbf{v}=\mathbf{v}^\mathrm{T}\mathbf{u}$，而 $\mathbf{X_v}d\boldsymbol{\theta}$ 和 $\mathbf{X_v}\boldsymbol{\theta}-\mathbf{y_r}$ 正是两个同维的列向量

$s$ 是关于 $\theta_j (j=0,1, 2, …, n)$ 的多元函数，我们知道多元函数的全微分公式为：

联立式 (3.9) 和式 (3.10)：

联立式 (3.8) 和式 (3.11)，很容易求得最优函数的多项式系数向量 $\boldsymbol{\theta}$：

相比代数法求解中的矩阵 $\mathbf{X}$ 和向量 $\mathbf{y}$，矩阵法中的矩阵 $\mathbf{X_v}$ 和向量 $\mathbf{y_r}$ 构造起来更加简单。仔细观察，可以发现：

说明两个解法是等价的。

4 代码实现

通过 C++ Eigen库实现了矩阵法中的求解方式，Eigen 版本为 v3.3.7，运行环境为 Windows10，Eigen 库安装路径为 D:\eigen-3.3.7。

函数声明

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#ifndef LEAST_SQUARE_METHOD_H
#define LEAST_SQUARE_METHOD_H

#include <D:\eigen-3.3.7\Eigen\Dense>
#include <vector>

using namespace std;

/**
 * @brief Fit polynomial using Least Square Method.
 *
 * @param X X-axis coordinate vector of sample data.
 * @param Y Y-axis coordinate vector of sample data.
 * @param orders Fitting order which should be larger than zero.
 * @return Eigen::VectorXf Coefficients vector of fitted polynomial.
 */
Eigen::VectorXf FitterLeastSquareMethod(vector<float> &X, vector<float> &Y, uint8_t orders);

#endif

函数实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include "LeastSquareMethod.h"

/**
 * @brief Fit polynomial using Least Square Method.
 *
 * @param X X-axis coordinate vector of sample data.
 * @param Y Y-axis coordinate vector of sample data.
 * @param orders Fitting order which should be larger than zero.
 * @return Eigen::VectorXf Coefficients vector of fitted polynomial.
 */
Eigen::VectorXf FitterLeastSquareMethod(vector<float> &X, vector<float> &Y, uint8_t orders)
{
    // abnormal input verification
    if (X.size() < 2 || Y.size() < 2 || X.size() != Y.size() || orders < 1)
        exit(EXIT_FAILURE);

    // map sample data from STL vector to eigen vector
    Eigen::Map<Eigen::VectorXf> sampleX(X.data(), X.size());
    Eigen::Map<Eigen::VectorXf> sampleY(Y.data(), Y.size());

    Eigen::MatrixXf mtxVandermonde(X.size(), orders + 1);  // Vandermonde matrix of X-axis coordinate vector of sample data
    Eigen::VectorXf colVandermonde = sampleX;              // Vandermonde column

    // construct Vandermonde matrix column by column
    for (size_t i = 0; i < orders + 1; ++i)
    {
        if (0 == i)
        {
            mtxVandermonde.col(0) = Eigen::VectorXf::Constant(X.size(), 1, 1);
            continue;
        }
        if (1 == i)
        {
            mtxVandermonde.col(1) = colVandermonde;
            continue;
        }
        colVandermonde = colVandermonde.array()*sampleX.array();
        mtxVandermonde.col(i) = colVandermonde;
    }

    // calculate coefficients vector of fitted polynomial
    Eigen::VectorXf result = (mtxVandermonde.transpose()*mtxVandermonde).inverse()*(mtxVandermonde.transpose())*sampleY;

    return result;
}

在函数实现中使用了一些 Eigen 的小技巧：

  • 使用 Eigen::Map 直接将样本数据由 std::vector 映射到 Eigen::VectorXf 参与运算，避免了循环数据读入
  • 通过 array() 方法累乘样本数据的 X 向量，逐列构造范德蒙矩阵，同样避免了大量的循环数据处理

拟合测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>
#include "LeastSquareMethod.h"

using namespace std;

int main()
{
    float x[5] = {1, 2, 3, 4, 5};
    float y[5] = {7, 35, 103, 229, 431};

    vector<float> X(x, x + sizeof(x) / sizeof(float));
    vector<float> Y(y, y + sizeof(y) / sizeof(float));

    Eigen::VectorXf result(FitterLeastSquareMethod(X, Y, 3));

    cout << "\nThe coefficients vector is: \n" << endl;
    for (size_t i = 0; i < result.size(); ++i)
        cout << "theta_" << i << ": " << result[i] << endl;

    return 0;
}

运行编译后的可执行程序，得到如下结果：

1
2
3
4
5
6
7
8
$ ./LSM.exe

The coefficients vector is:

theta_0: 1.30698
theta_1: 0.924561
theta_2: 2.0032
theta_3: 2.99976

点击这里下载完整的工程 Demo，工程使用了 cmake 编译链，你也可以下载工程后使用其中的程序文件创建符合自己开发习惯的工程。

5 总结

本文中的矩阵法本质在于，通过样本集构造范德蒙德矩阵，将一元 N 次多项式非线性回归问题转化为 N 元一次线性回归问题（即多元线性回归）。对于线性回归问题的求解，Eigen 库中有多种实现：

  • LU 分解
  • 基于 Householder 变换的 QR 分解
  • 完全正交分解（Complete Orthogonal Decomposition，COD）
  • 标准 Cholesky 分解（LLT）
  • 改进型 Cholesky 分解（LDLT）
  • SVD 分解

不同方法在对矩阵 $\mathbf{A}$ 的需求、求解速度、求解精度上有所差异，Eigen 官网对几种方法进行了对比总结，查看原文请移步 Linear algebra and decompositions 。

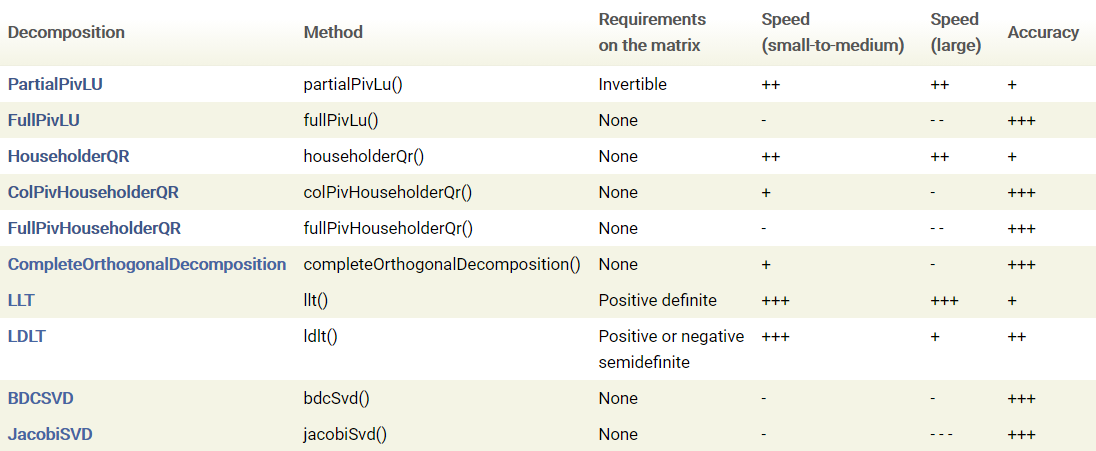
Eigen 库中线性问题的几种求解方法对比

Eigen 官网在 Solving linear least squares systems 章节中讨论了 SVD 分解、QR 分解和正规方程（即使用 LDLT 解法）三种方法在求解线性最小二乘问题上的差异，并指出：SVD 分解通常精度最高但速度最慢，正规方程速度最快但精度最差，QR 分解性能介于两种方法之间。相比 SVD 分解和 QR 分解，当矩阵 $\mathbf{A}$ 病态时，正规方程解法所得结果将损失两倍精度。

利用上文所述的工程 Demo 中的小样本（三次多项式 $f(x) = 1 + x + 2x^2 + 3x^3$ 附近的 5 个点）构造出范德蒙德矩阵（即矩阵 $\mathbf{A}$）后，对矩阵法（文中方法）、正规方程、householderQr 分解和 bdcSvd 分解进行了拟合实验对比：

几种求解线性最小二乘问题方法的对比

从结果可以看出，在求解速度方面：

在求解精度方面：

householderQr 分解综合性能较优，矩阵法综合性能较差，且有 $\mathbf{A}^\mathrm{T}\mathbf{A}$ 可逆的要求。

对于线性回归问题，还可通过梯度下降法进行求解，梯度下降法具体使用中还会涉及一些工程细节，例如数据的特征缩放（归一化）、步长 $\alpha$（学习率）的选择、迭代次数的设置等，具体不再展开，后面会另开一篇文章。

参考

  1. 如何理解最小二乘法？
  2. 最小二乘法拟合多项式原理以及 c++实现
  3. 最小二乘法多项式曲线拟合原理与实现
  4. 最小二乘法多项式曲线拟合原理与实现（数学公式详细推导，代码方面详细注释）
  5. c++ 曲线拟合的最小二乘法 公式 二次多项式和三次多项式
  6. 最小二乘法
  7. 最小二乘法（least sqaure method）
  8. Linear algebra and decompositions
  9. Solving linear least squares systems
  10. 机器学习：用梯度下降法实现线性回归
  11. 机器学习：最小二乘法、最大似然估计、梯度下降法
  12. 最小二乘法和梯度下降法有哪些区别？
  13. 最小二乘法与梯度下降的区别
  14. 最小二乘法与梯度下降法的区别？
  15. 从线性回归到最小二乘法和梯度下降法
  16. 如何直观形象的理解方向导数与梯度以及它们之间的关系？
  17. 使用最小二乘法和梯度下降法进行线性回归分析
  18. 矩阵求导术（上）
猜你喜欢
Thank you for your donate!